To What End Do We Study Riemann’s Investigation of Abelian Functions?
by Bruce Director
On June 10, 1854, Bernhard Riemann shocked the world by stating the obvious:
For more than two thousand years scientists had accepted, as dogma, that the axioms of Euclidean geometry were the only foundation for science, despite the fact that science had been left in the dark as to whether these axioms had any physical reality. “From Euclid to Legendre, to name the most renowned writers on geometry, this darkness has been lifted neither by the mathematicians nor by the philosophers who have labored upon it.” The axioms of Euclidean geometry are, Riemann said, “like all facts, not necessary but of a merely empirical certainty; they are hypotheses; one may therefore inquire into their probability, which is truly very great within the bounds of observation, and thereafter decide concerning the admissibility of protracting them outside the limits of observation, not only toward the immeasurably large, but also toward the immeasurably small.”
Though Riemann’s words were welcomed by the aged Gauss, (who had long held but rarely publically stated this view), they were inimical to the Kantianism that had come to dominate a significant part of European science since the oligarchy’s suppression of Benjamin Franklin’s Leibnizian allies, that had accelerated with the French Revolution and its aftermath. Kant and his successors had preached the evil doctrines of a hermetic separation between the workings of the mind and the physical world, and, a hermetic separation within the mind between scientific and artistic thinking. The former dictated that man was doomed to impose on the physical world the axioms of Euclidean geometry, no matter what physical evidence contradicted it. The latter insisted that man’s mental processes were limited either to the cold logic that Kant falsely attributed to science, or the unknowable irrationality that he erroneously described as art.
As a proponent of Friedrich Schiller’s collaborator Herbart, and a student of Abraham Kaestner’s protege Gauss, Riemann saw through these Kantian sophistries. Like Plato, Cusa, Kepler and Leibniz before him, Riemann recognized that though sense perception cannot tell us anything truthful about the physical universe, the mind’s power to form hypotheses can. Following Herbart, Riemann noted that such hypotheses are not formed {a priori} as Kant insisted, but only by the mind’s investigation of physical causes. These hypotheses, Riemann emphasized, must be constantly improved, “under the compulsion of facts that it cannot explain.”
Thus, scientific progress occurs through a succession of paradoxes which challenge the prevailing way of thinking. As Riemann wrote in his posthumously published philosophical fragments:
“Natural science is the attempt to understand nature by means of exact concepts.
“According to the concepts through which we comprehend nature, our perceptions are supplemented and filled in, not simply at each moment but also future perceptions are seen as necessary….
“To the extent that what is necessary or probable, according to these concepts, takes place, then this confirms the concepts, and the trust that we place in these concepts rests on this confirmation through experience. But if something takes place that is unexpected according to our existing assumptions, i.e., that is impossible or improbable according to them, then the task arises of completing them or, if necessary, reworking the axioms, so that what is perceived ceases to be impossible or improbable. The completion or improvement of the conceptual system forms the `explanation’ of the unexpected perception. Our comprehension of nature gradually becomes more and more complete and correct through this process, simultaneously penetrating more and more behind the surface of appearances….
“Herbart furnished the proof that concepts that allow us to comprehend the world…can be derived from this source (physical paradoxes–bmd), in so far as they are more than mere forms combining simple sense images; and therefore these concepts need not be derived from some special constitution of the human mind which precedes all experience (such as Kant’s categories).”
Thus truthful hypotheses can only arise from physical paradoxes. Yet these paradoxes will not be recognized if the mind is girdled by an {a priori} dogma, such as Kant’s insistence on the primacy of Euclidean geometry. Consequently, Riemann admonished his colleagues, they must be willing to reflect on the general notions by which hypotheses concerning physical processes are formed, so that, “the task shall not be hindered by too restricted conceptions, and that progress in perceiving the connection of things shall not be obstructed by the prejudices of tradition.”
Here again Riemann is in direct contradiction to Kant. For the formation of new hypotheses, by their very nature, must lie outside the “logic” of any existing system of axioms, postulates and definitions. Therefore, Kant’s insistence that scientific knowledge is limited to a logical system, limits knowledge. Scientific progress occurs through the {creation} of new thoughts, in response to a conflict between existing thoughts and the physical world. This conflict provokes an emotional response in the mind of the scientist: “a powerful sense of wonder that drives men to look into causes,” as Kepler described it. Progress occurs, contrary to Kant, because this creative process, for both the scientist and artist alike, can be, and is, known.
Lyndon LaRouche’s unique discoveries in the science of physical economy provide the only fully elaborated conception for the knowability of the creative process. It is in this vein, and from this higher standpoint, that Riemann’s investigations of the complex domain must be approached. A pedagogical investigation into Riemann’s treatment of Abelian functions acquaints us both with the physical paradoxes that provoked Riemann’s thought, and an insight into the creative process that enabled him to make the discovery.
The Relationship of Mind and Physics
Riemann’s approach was in the tradition of Pythagorean Sphaerics. When ancient scientists invented the sphere they were not describing a physical object. No one saw, in the sky, a great sphere. Yet as these ancients moved their eyes around the sky, seeking to gain a greater mastery over the world in which they lived, the idea of the sphere was born. Its form expressed both the manifold of action on which the ever-changing physical motions were projected into the visible domain, {and}, the active relationship between these motions, and the minds that were investigating their causes. It was, as Kepler later said, a first assumption of reason, which, once conceived, secured a conceptual platform from which deeper investigations could be pursued. That deeper knowledge could be acquired, not by new experience alone, but only when the investigators themselves recognized that such new experience obliged them to change the platform on which they were standing.
From this new platform, these celestial motions were seen not to conform to the perfect circles which were characteristic of spherical action, but to another, more complex mode of action. An early effort to grasp this higher mode of action is expressed by Archytas’s construction for the doubling of the cube. There he demonstrated that the cube, which is derived from the sphere, cannot be doubled within the spherical domain, but only from the domain of the multiply-connected action from which the torus, cylinder and cone are unfolded. When Kepler discovered the harmonically ordered elliptical nature of planetary orbits, he was confirming that it was this higher manifold of action, expressed by Archytas’s solution to doubling the cube, which was, in fact, the one that characterized the planetary motions, whose visible projections were traced on the celestial sphere.
This is the spirit with which to approach the geometry that bears Riemann’s name. No one has ever “seen” a Riemann’s surface, nor does such a surface describe the visible appearance of some physical effect. Rather, like the ancients’ celestial sphere, Archytas’s torus, cylinder and cone, or Kepler’s harmonically ordered elliptical orbits, Riemann’s surface expresses {the relationship between the physical principles, their sensible effects, and our investigating minds}.
There is, of course, an entire class of physical investigations, in which Riemann was deeply and actively involved, whose understanding he advanced by applying his concept of the complex domain, including problems in geodesy, geomagnetism, astronomy, electrodynamics, and hydrodynamics. But it was not merely the practical solutions that Riemann sought. Such practical solutions, Riemann emphasized, flowed only from the change in thinking required to discover the principles upon which such physical effects depend–a change in thinking congruent with that experienced in his treatment of Abelian functions.
Just as Plato instructed the Delians to disregard the practical applications of doubling the cube and to focus instead on the cognitive improvements gained from its investigation, Riemann advised the scientists of his day not to focus merely on methods for calculating the transcendental functions, that Leibniz had shown, were the functions on which all physical action was based. Instead, as Riemann noted in his 1857 treatise on Gauss’s “Hypergeometric Function” , it is because of the numerous applications of these transcendental functions to physical and astronomical investigations, that a suitable representation of their universal characteristics must be given. It is from this standpoint, Riemann emphasized, that the calculations can be derived.
In solving the problem of doubling the cube, the Greeks did not get bigger altars. They got better minds. In designing his surfaces, Riemann did not create a new means of computing. He created a new means of thinking, and, just as important, laid the foundation for its successor.
The Physical Foundation of Complex Functions
Though the physical necessity of complex numbers was first indicated by Leibniz, Gauss was the first to elaborate their rigorous foundations. In his earliest notebook entries, his letters to collaborators, and his published statements on the subject, Gauss always emphasized that the significance of complex numbers was not their mathematical properties. Rather, the mathematical properties of complex numbers were only significant because they reflected physical characteristics.
Illustrative of this view is Gauss’s 1809 pedagogical exercise, “Questions Concerning the Metaphysics of Mathematics”, in which he states that “mathematics in the most general sense is the science of relationships…” Then, after sketching the mathematical properties of complex numbers, which he describes as quantities that express “a relationship between relationships”, Gauss concludes this short note by emphasizing that “it would be extremely important to bring to light this theory inversely {without quantity}.” He then describes the motion of the spirit bubble in a plane leveller, as a physical example of what mathematics would call a “complex number”.
Gauss included a statement of the physical foundation for complex numbers in his 1832 “Second Treatise on Bi-quadratic Residues”, the which was cited by Riemann in his habilitation dissertation. There Gauss identified complex numbers explicitly as {anti-Kantian}, insisting that the very idea of complex numbers cannot even {arise} in the mind, nor be communicated, {a priori}. Complex numbers, Gauss repeatedly emphasized, arise only from the investigation of physical processes. It is polemically ironic that Gauss would declare these physical foundations for complex numbers in a treatise dedicated to the theory of numbers, a subject that his enemies (and most academic fools today) would regard as the domain of “pure mathematics”.
The physical foundation of complex numbers, for Gauss, was not simply a matter of philosophical interest. His unequaled accomplishments in geodesy, astronomy, geomagnetism, potential theory and conformal mapping, all employ this quality to obtain physical results. Certain aspects of Gauss’s work in this regard have been treated in previous installments of this series and more will be treated in the future. However, for purposes of the present discussion, it is relevant to illustrate this physical basis for complex functions from the standpoint of Riemann’s investigation of the relationship of complex functions and surfaces of physical least-action known as minimal surfaces, typified by the catenoid.
Riemann’s discovery depends on Gauss’s method of spherical mapping, which itself, was a generalization of the method of Pythagorean Sphaerics. Over the ages, astronomers had measured the relationship between the positions of stars on the celestial sphere from different positions on the Earth. Such measurements were normalized by measuring the angle of inclination of a star with respect to the direction of a plumb bob. Through his work on geodesy, Gauss recognized that the plumb bob points in the direction of the pull of gravity, and that the unseen, but actual, surface of the Earth, is that surface that is everywhere perpendicular to this direction. Thus, as the plumb bob is moved from place to place around the Earth, its changing direction reflected the changing curvature of the Earth’s, unseen, gravitational surface. This changing curvature is, in turn, reflects on the celestial sphere by changes in the stars’ angles of inclination as measured from different positions on the Earth. In sum, the irregular changing curvature of the Earth is mapped onto the regular curvature of the celestial sphere.
Using this same approach, of mapping the changing directions of a normal to a surface onto a sphere, Gauss established a standard for measuring the curvature of any arbitrary surface. Such maps are now called “Gauss spherical mappings”.
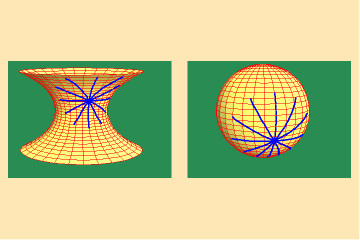
This mapping is illustrated in animated figures 1 for the case of the spheroid.
The left panel of the animation shows a normal moving around a curve on the spheroid. As the normal moves, its changing direction reflects the changing curvature of the spheroid. In the right panel the changing directions of this normal are mapped onto a sphere by a moving radius whose direction is always parallel to the moving normal on the spheroid. Gauss used the area of the spherical image as a measure of the curvature of the original surface. The greater the variation in the curvature of the surface, the greater the area of its spherical image, and vice versa.
Riemann focused on the unique characteristic of these Gauss spherical mappings for surfaces of physical least-action, such as the catenoid. For such surfaces, Riemann showed, the Gauss spherical map was always conformal.
This is illustrated in figures 2a and b.
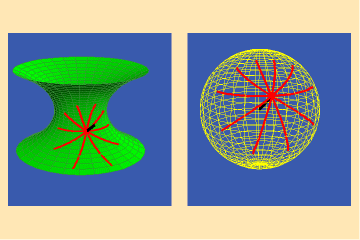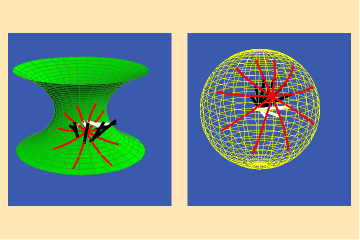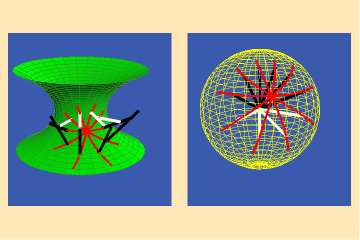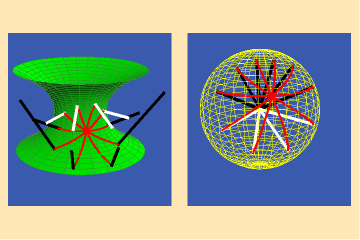
Here we see the Gauss map of a collection of curves on a catenoid that intersect at equal angles. Notice that the images of these curves in the Gauss spherical map also intersect at equal angles. Hence, the Gauss spherical map of the catenoid preserves angles, i.e., it is conformal.
This is not the case for other surfaces, such as the hyperboloid illustrated in figures 3a and b, and the spheroid illustrated in figures 4a and b.
3 a,b
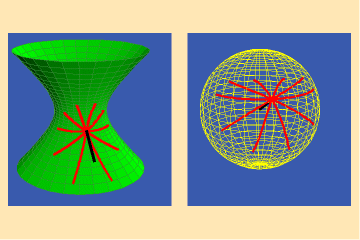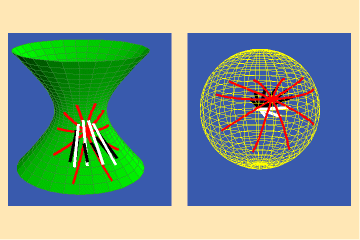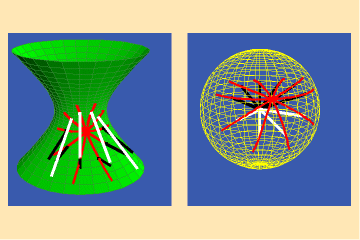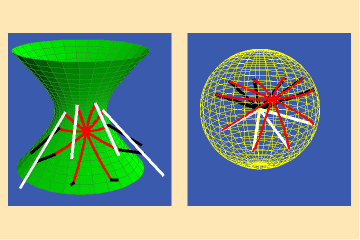
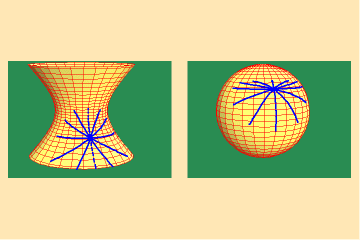
4 a,b

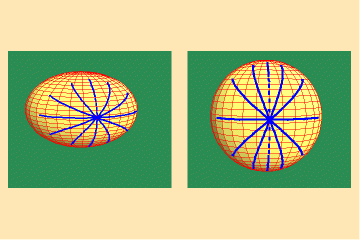
In both cases the curves on the surface intersect at equal angles, but the angles between their images on the spherical maps are different. Hence, the Gauss spherical maps for these surfaces are not conformal.
Riemann recognized that the conformality of the Gauss spherical maps of minimal surfaces reflects the unique physical least-action characteristic of such surfaces–specifically, that the rate of change of the curves of minimum and maximum curvature is equal, or, in other words, the minimum and maximum curves were harmonic. (See Riemann for Anti-Dummies 58 and 60.) It is important to emphasize that this harmonic relationship is an effect, not a cause. The physical principle of least-action is the cause. That physical principle is expressed, mathematically, in the harmonicity of the minimum and maximum curves, and the conformality of the Gauss spherical maps. But this mathematical property is not significant for abstract mathematical reason. It is significant because it reflects a physical characteristic and in so doing, assists us in forming, and communicating, a concept of the essential characteristics of that physical principle.
But, now Riemann went the next step and inverted the question. Following Gauss, Riemann understood that complex functions, when represented geometrically on a surface, produce conformal mappings. Consequently, any complex function could be thought of as a Gauss spherical map of some physical least-action surface. Such surfaces were not necessarily visible objects. Rather, they expressed manifolds of physical least-action, whose shadow, in the visible domain, is a conformal map. Riemann showed we can work backwards from these conformal maps to construct an image of the physical manifold of least-action. Such images take the form of a Riemann’s surface.
The Physical Foundation of Abelian Functions
The physical characteristic of complex functions, illustrated above for minimal surfaces, is just a particular example of the more general case of which Riemann spoke in his habilitation dissertation. There he poses the questions, and proposes the direction by which the true determination of physical relationships can be discovered. Once we have rejected any {a priori} axiomatic assumptions, on what do we rely for the determination of physical relationships? If we rely on the relationships among objects of sense, we will know nothing about the universal principles that lie outside the sensorial domain. But, Riemann emphasized, if we cannot rely on the relationships observed among the objects of sense, the basis for physical relationships “must be sought for outside that actuality, in the colligating forces (Kraeften) that operate upon it.”
By colligating forces, Riemann is referring to the universal physical principles, which, being universal, are acting everywhere on the visible domain from outside. As Leibniz showed in the initial development of the infinitesimal calculus, the relationships among the discrete objects of the visible domain are determined by the continuous, but differential, action of universal principles. Riemann extended Leibniz’s notion, hypothesizing that when a physical process is the effect of a multiplicity of universal principles, those principles can be thought of as constituting a multiply-extended continuous manifold. But these universal principles are not sensible. Therefore, Riemann said, “there are in common life only such infrequent occasions to form concepts whose modes of determination form a continuous manifold, that the positions of objects of sense, and the colors, are probably the only simple notions whose modes of determination form a multiply-extended manifold. More frequent occasion for the birth and development of these notions is first found in higher mathematics.”
In particular, Riemann notes, such concepts of multiply-extended continuous manifolds arose in connection with his investigation of Abelian functions. To further our understanding of these manifolds, Riemann developed his method of representing them as Riemann’s surfaces.
These Riemann’s surfaces, like the Pythagorean sphere, Archytas’s construction, or Gauss’s surfaces, are not visible objects. They are the metaphorical images of thought-objects that express the relationships of a multiplicity of insensible universal principles which are acting together to produce a physical effect.
From this standpoint, Riemann was able to demonstrate that the essential characteristic of a multiply-extended continuous manifold is determined by the density of singularities that that manifold could sustain. This density of singularities, therefore, indicates the physical “power” or “potential” of the manifold. Just as Gauss expressed the power of an algebraic equation by a geometrical characteristic, Riemann showed that the power of a species of functions can be expressed by the geometrical characteristics of the Riemann’s surface. These species characteristics, Riemann emphasized, are the primary determinant of potential action in a physical manifold while other factors, such as variations among different functions of the same species, are of relatively little importance.
To better understand this concept, it is pedagogically most efficient to work through a series of animations illustrating Riemann’s surfaces, associated with manifolds of action of increasing density and power. Each type of Riemann’s surface is illustrated through an ordered series of animations, comprised of groups of triple-pairings showing the various characteristics of the surface from three different viewpoints: flat, 3D and stereographic projection. Each pair of animations shows an animated trajectory within a continuous manifold of physical action, and the effect on that trajectory of a complex function. To grasp the concept of the Riemann’s surface, the viewer must form a single idea of the effect of the function from the three pairs of animations. The function is not depicted directly in any of the animations. What is depicted is merely the effect. {The function is the concept, formed in the mind, of the characteristics of the principle which has the power to produce the depicted effect}.
However, as Riemann stressed, the change in density of singularities expressed by a Riemann’s surface depends, not on the particular function, but only on the {species} of function (i.e. algebraic, transcendental, elliptical, hyper-elliptical, etc.). Therefore, what is important to know is not the characteristics of any particular function, but the characteristics of a species of functions, and even more importantly, the characteristic of change from one species of function to a higher species.
This is illustrated in the animations by grouping an entire set of tripled-pairs into an ordered series illustrating the characteristic of an entire species. That characteristic is not directly depicted visibly in the animations. Rather it is evoked as a concept (thought-object) when the mind recognizes the total potential of that species to produce a change in the action. {It is this cognitive act, not the visible form, that constitutes the concept of the complex function}.
In this way, the entire set of animations walks the viewer through a succession of cognitive leaps. First, the leap required to put a pair of animations together. Then the leap required to put a tripled-pair into a unified idea. Then, the leap from one tripled pair to the next within a species. Then, the leap from species to species. Thus, it is not any single animation that presents the idea, but the cognitive change that is evoked as the viewer moves from one pair, to the triplet, from triplet to triplet, and from species to species. The animations themselves are not the idea. They are the vehicles by which the idea is evoked in the mind of the viewer. The viewer can then reflect on the succession of thought-objects that have been evoked through an investigation of the succession of animations. Reflecting back on the entire succession, the viewer can then form a single idea–a mental animation–of the different qualities of change embedded in the process.
It is this {change of change} that forms an initial idea of Riemann’s concept of Abelian functions.
What follows is a series of animations selected from a larger series that was presented at the recent February 22, 2005 cadre school. (The entire series can be downloaded from http://wlym.com/animations/riemann61.zip ).
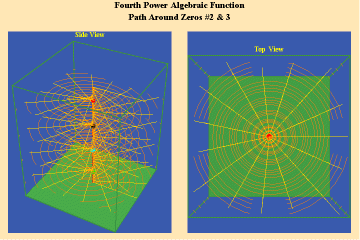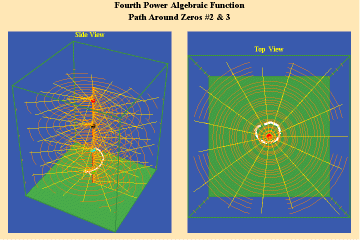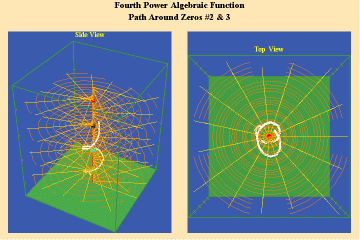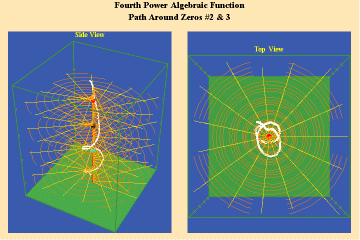
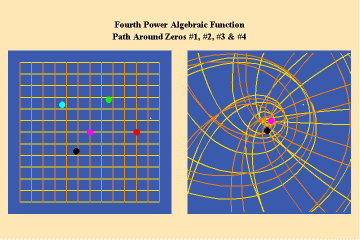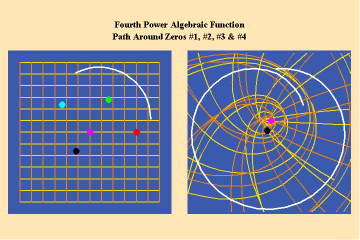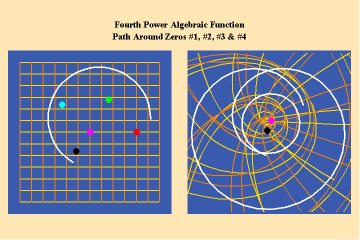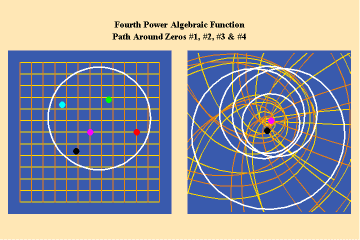
Animations 5a,b, c; 6 a, b, c: and 7 a, b, c; illustrate the effect on a closed trajectory encircling, none, two and four singularities, with respect to an algebraic function.
5 a,b,c

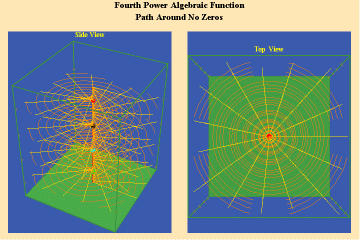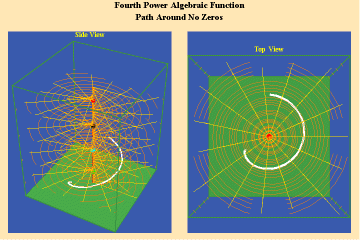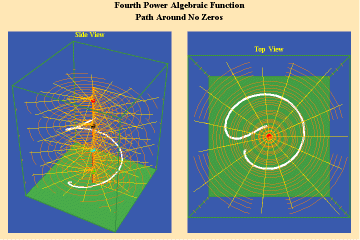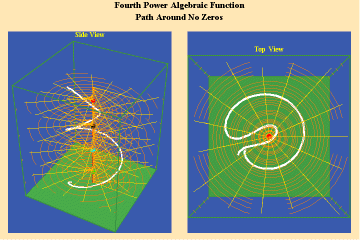

6 a,b,c

7 a,b,c
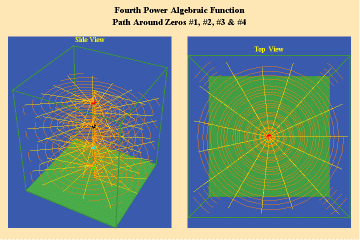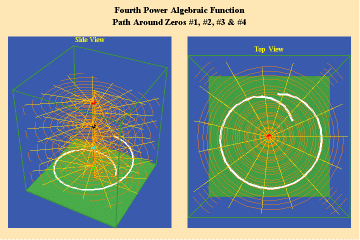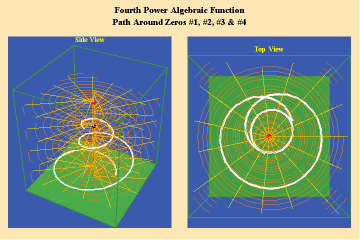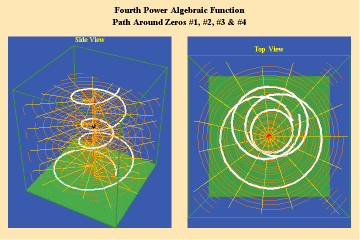

The effect of the manifold of action on this trajectory is to increase the number of rotations by the number of singularities encircled. Since, in this example, the function is a fourth power algebraic function, the maximum potential for change is a quadrupling of effect.
Animations 8a, b; show a different algebraic species of function with an additional, but different, type of singularity–a pole.
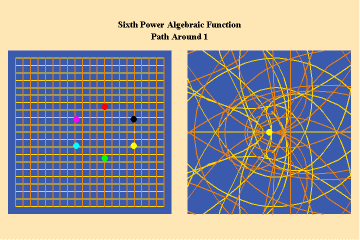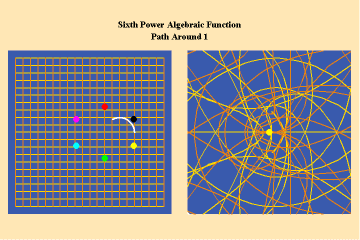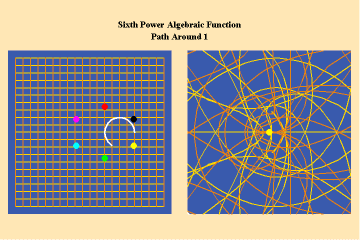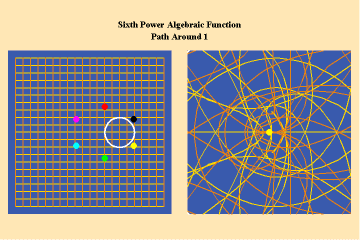
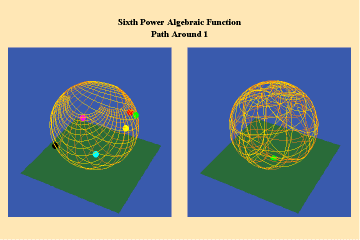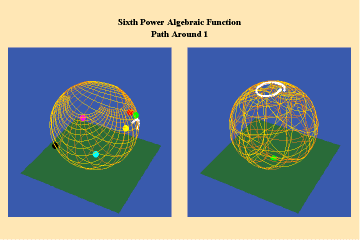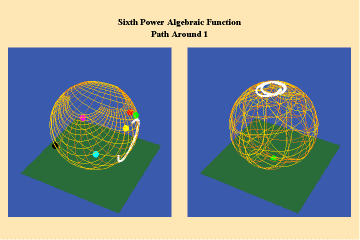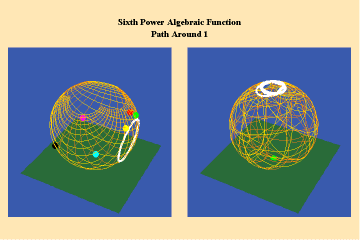
The effect of this type of singularity (pole) can only be seen in the stereographic, spherical view. Here we see the importance of Riemann’s insistence on representing his surfaces in spherical form. By using the stereographic projection, we can see the total potential of the function– even those effects which, in the plane, might not be evident because they appear to be “infinitely” far away. Riemann’s approach, like Cusa’s, treats the “infinite” not as an indication of something outside the universe, but merely an indication that something is outside our conceptual ken. With Riemann’s stereographic mapping we rise above that apparent limitation and recognize that it had only existed because of a mind-deadening acceptance of Kant’s insistence on the primacy of Euclidean geometry.
A single trajectory around this singularity is transformed into a triple action around the “infinite”, which is represented by the north pole of the sphere in the stereographic projection.
Figure 8c depicts this relationship from the standpoint of a Gauss surface.
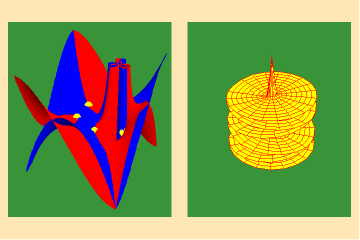
From these four triplets, we can already form an idea of the essential characteristic of the entire species of algebraic functions. As discussed in the last installment, the number of sheets of a Riemann’s surface of an algebraic function is determined by the power of the function. Thus, though any species of algebraic function will have the potential to increase the effect of an action, depending on how many singularities (roots or poles) that function can sustain, that potential will always be finite. Further, as is evident from the spherical view, all the roots will map to south pole of the sphere and all the poles will map to north pole. Thus, the Riemann’s surface for any algebraic function will have only two branch-points, and a finite number of branches.
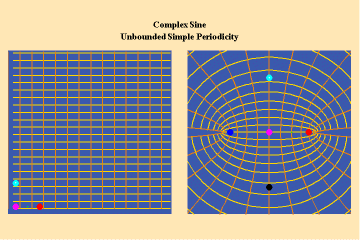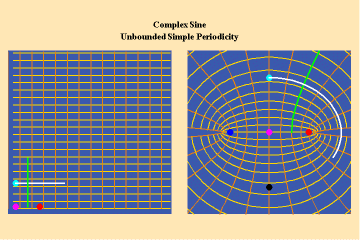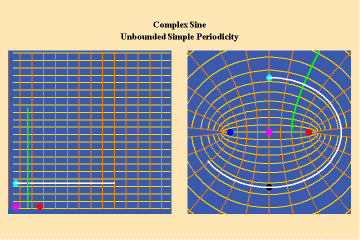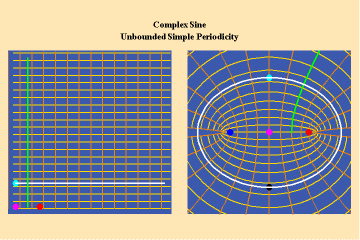
This limitation of a finite potential is only overcome (transcended), by the higher species of function–the simple transcendental function. This species is comprised of the exponential, circular and hyperbolic functions. Again, the essential characteristics of these functions, which are manifest physically by the catenary principle of least-action, are easily grasped when viewed from the standpoint of the relevant Riemann’s surface. These surfaces are depicted in animations 9a, b, c; 10, a, b, c: and 11 a, b, c; which illustrate a complex circular function (sine).
9 a,b,c

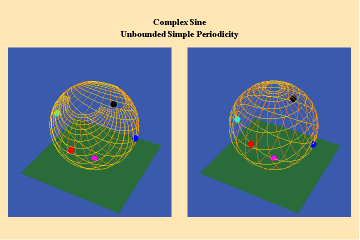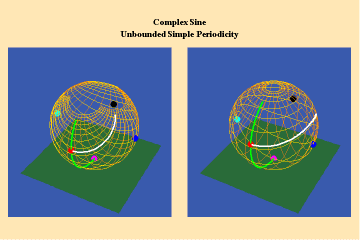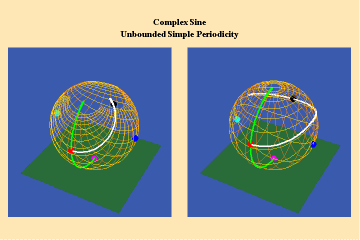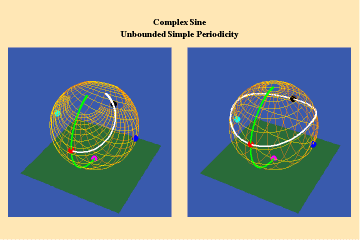
10 a,b,c
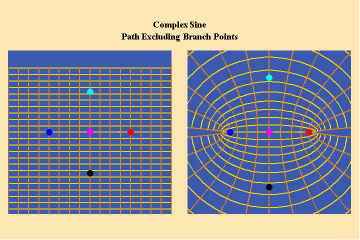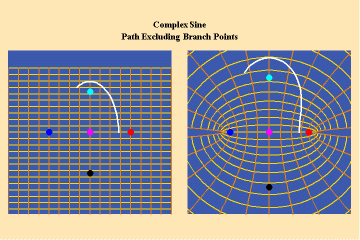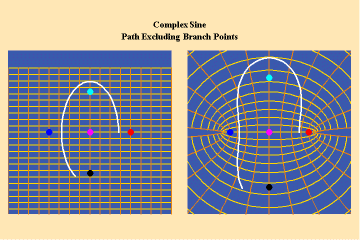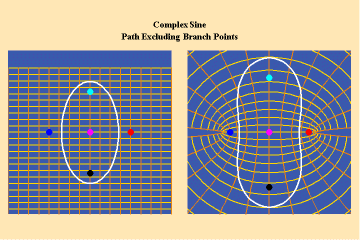
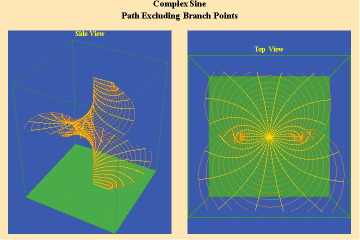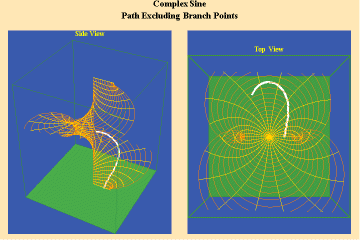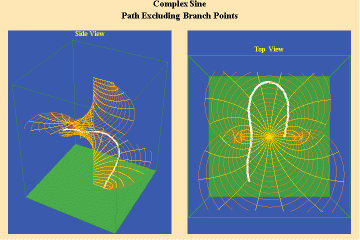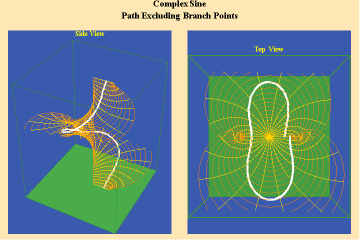
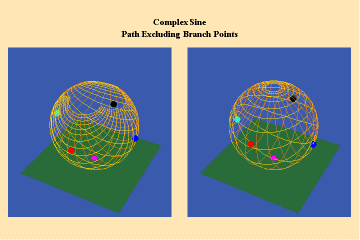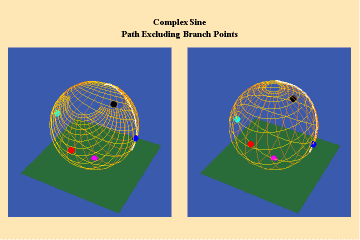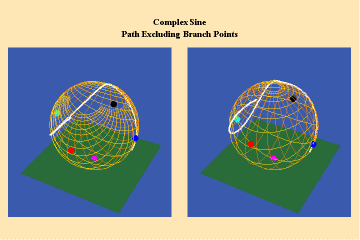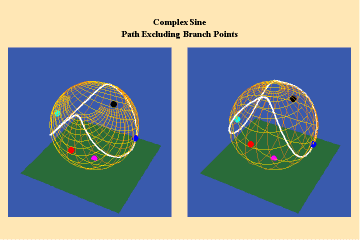
11 a,b,c
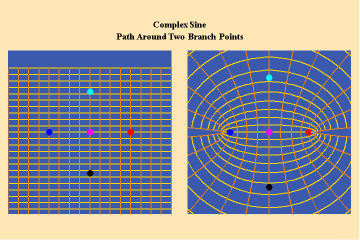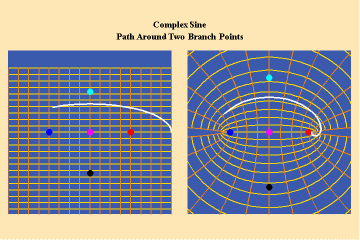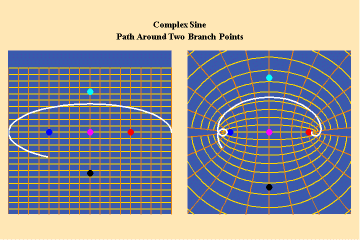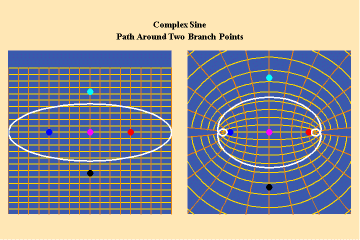
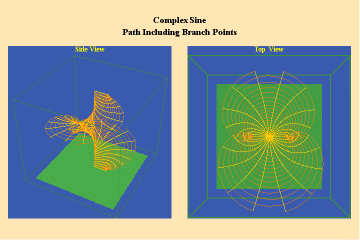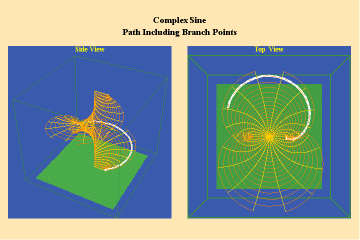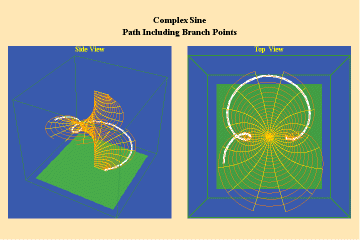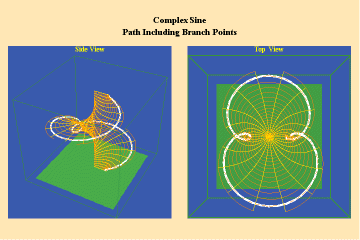
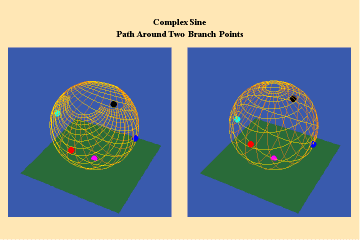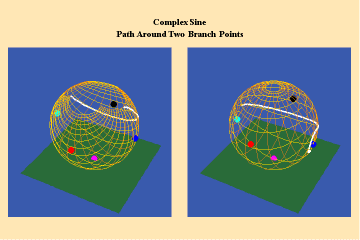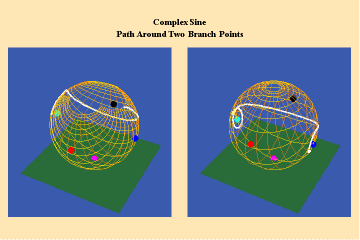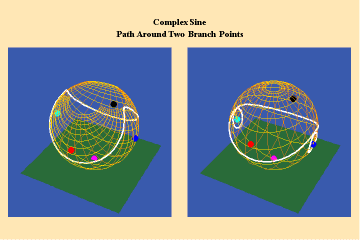
These functions are distinguished from the algebraic because they have an unbounded potential. This can at first be illustrated in animations 9, which shows the effect of a transcendental manifold on two perpendicular trajectories. In the left panels both trajectories appear to extend into the “infinite”. But in the right panel, one of the trajectories is transformed into a periodic ellipse. The unbounded nature of this periodicity can be seen in the stereographic view (9c). In the left, both trajectories are seen to approach the “infinite” represented by the north pole. On the right, the image of one of these trajectories becomes periodic, while the other remains aperiodic. Since the periodic trajectory is an image of an process on the left that is unbounded, its periodicity is also unbounded.
From this geometry we can see that a Riemann’s surface of this species of function will have two branch points, but an unbounded number of branches. Hence, it expresses a greater power for action than any possible algebraic function.
Animations 10 show a trajectory that encircles no branch points. Animations 11 shows a trajectory that encircles two branch points, producing a doubling effect around each branch point.
From these three triplets we can form a concept of the power of this simplest species of transcendental. It surpasses the power of the algebraic because its power is unbounded. But it exhibits a new type of boundary, specifically, the limit imposed by having only two branch points.
This new type of boundary is overcome by the next species of transcendental–the elliptical transcendental. This transcendental species is associated with a manifold of physical action in which two universal principles combine to produce one single effect. As, for example, in the case of elliptical motion in which motion along the arc of the ellipse is incommensurable with both the sine and the angle (as distinct from circular motion in which the arc is incommensurable with the sine, but commensurable with the angle).
Riemann showed that the essential characteristic of the elliptical transcendentals is expressed by the double periodicity of the action on the Riemann’s surface. (Gauss had already discovered this property by 1798, but never published his results. The extent of his work in this area was not publically known until the 1890’s.)
Like the simple transcendentals, but unlike the algebraic, the elliptical transcendentals have an unbounded potential. But, the elliptical transcendentals surpass the power of the simple transcendentals because they are doubly-periodic. This characteristic is depicted in animations 12 a, b, c;
12 a,b,c
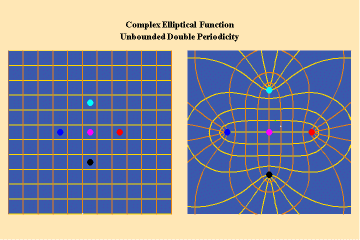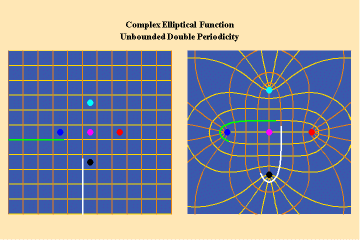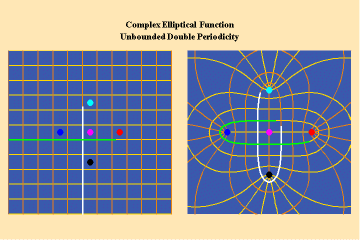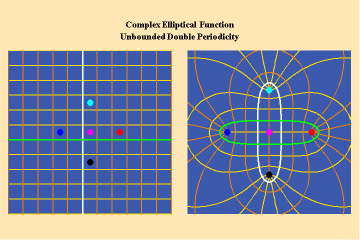
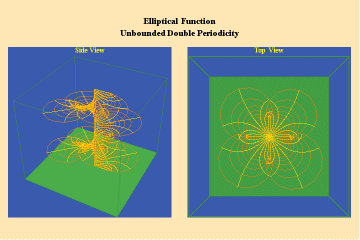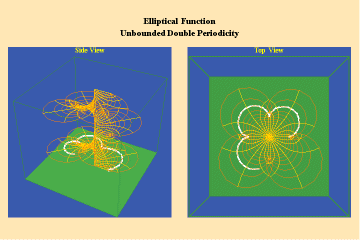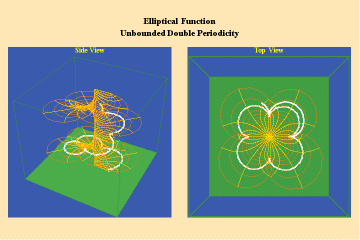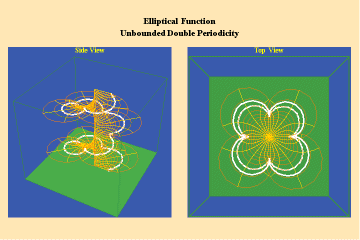
This triplet depicts two perpendicular trajectories which, in the left panels, appear to go off into the “infinite” being transformed into unbounded but periodic trajectories, as depicted in the right panels. Again, this characteristic can only be truly grasped from the viewpoint of the stereographic projection. This double periodicity of the elliptical transcendental produces, in the Riemann’s surface, four branch points and an unbounded number of branches.
Animations 13 a, b, c; 14 a, b, c; and 15 a, b, c; illustrate a trajectory within this elliptical manifold circling two branch points, two different branch points and all four branch points respectively.
13 a,b,c
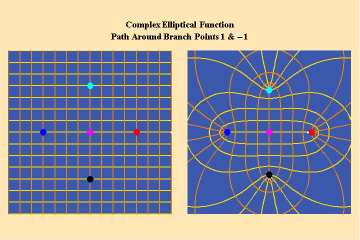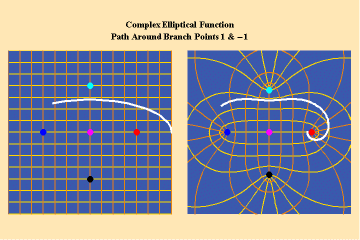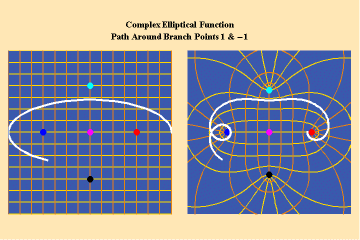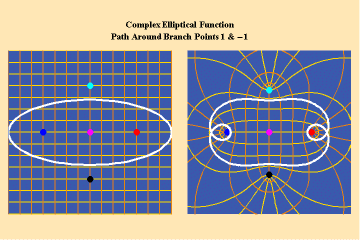

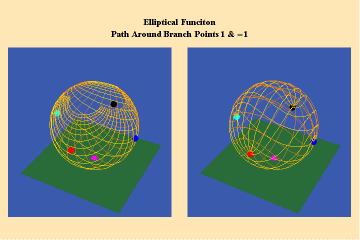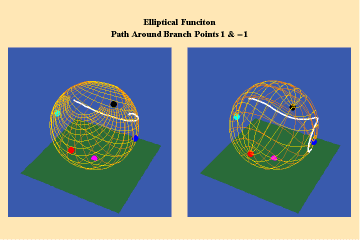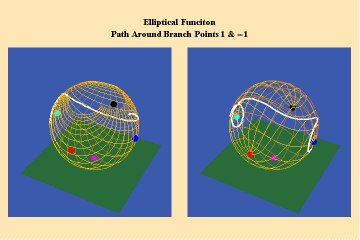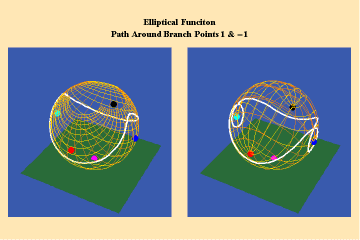
14 a,b,c
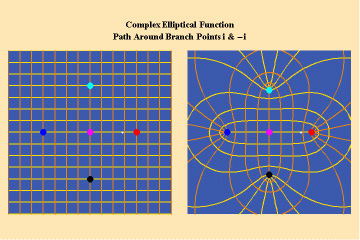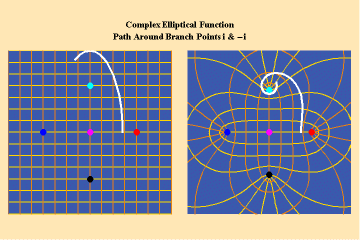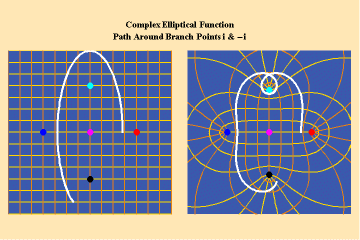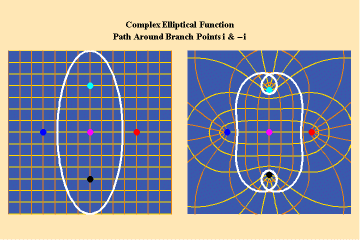
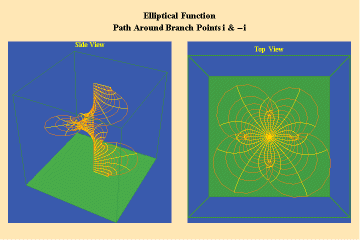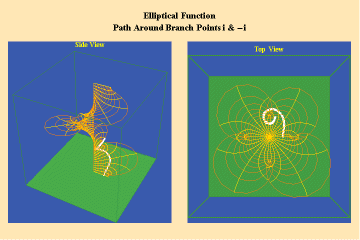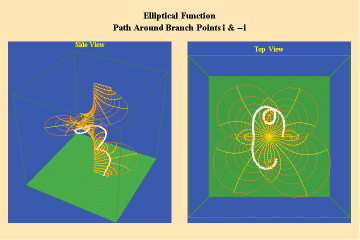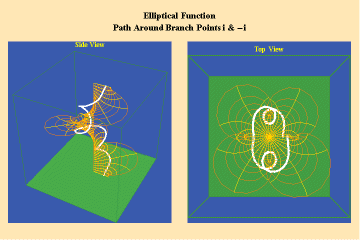
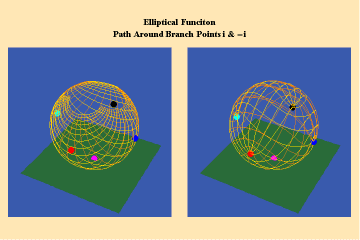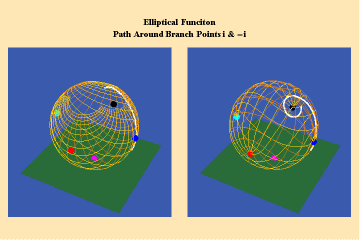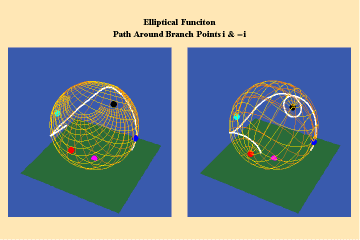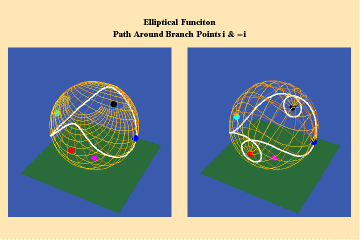
15 a,b,c
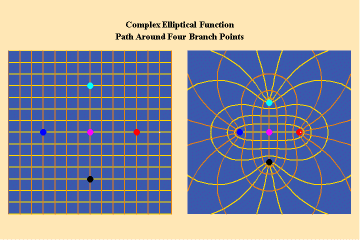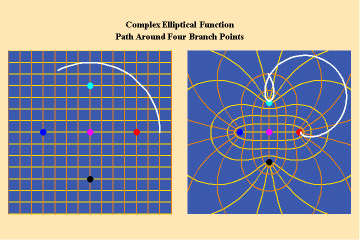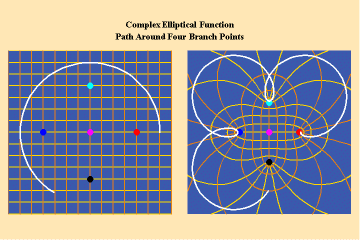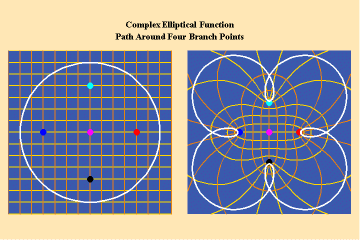
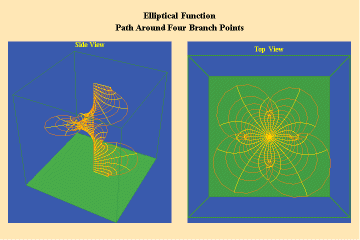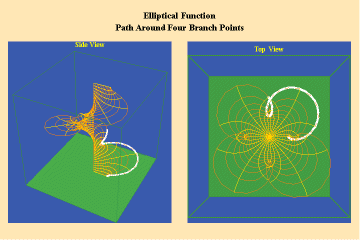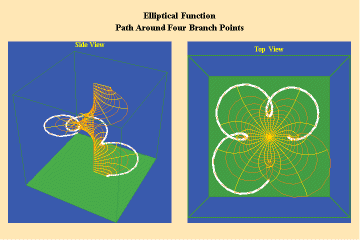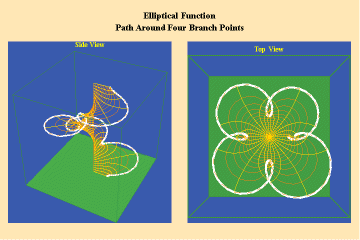
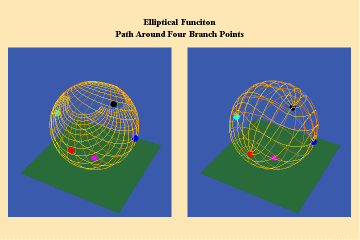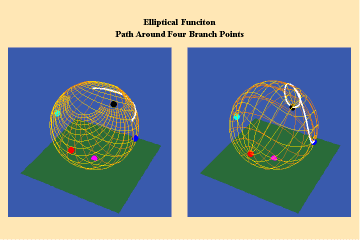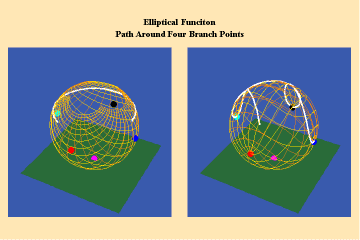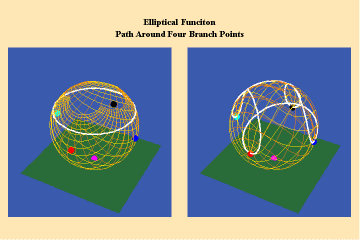
From this standpoint, it can be easily seen that manifolds of physical action characterized by the elliptical transcendentals, having the potential to sustain a greater number of singularities (branch points), have a potential to produce a greater physical effect and, as such, are of a higher power than the simple transcendentals.
Finally, think back on this entire process, from a standpoint above the characteristics of each particular species of function. Think of the power of mind by which you can conceive of an entire species of functions by their power to sustain a greater density of singularities and thus a greater power to produce a physical effect. Think of the power of mind by which you can conceive of the power to change from one species to the next higher species. Think of the power of mind by which you can extend this thought beyond the elliptical and into that extended class of transcendentals now known as Abelian functions.
That is the power of mind through which, “progress in perceiving the connection of things shall not be obstructed by the prejudices of tradition.”
