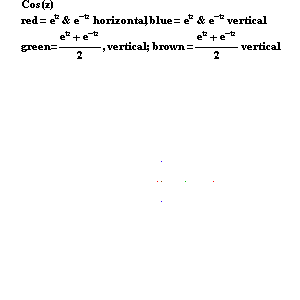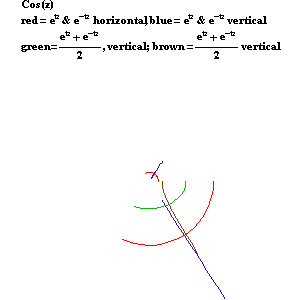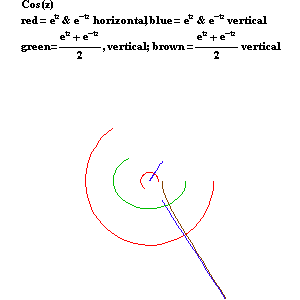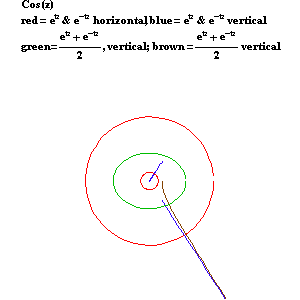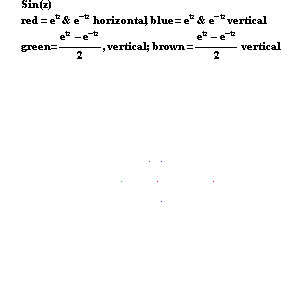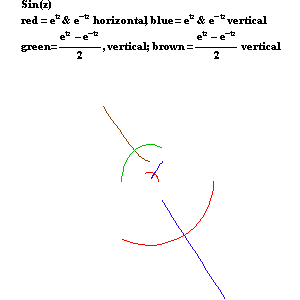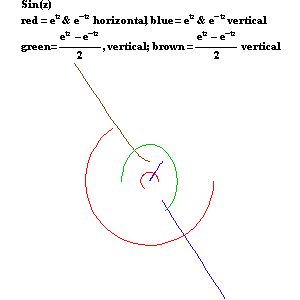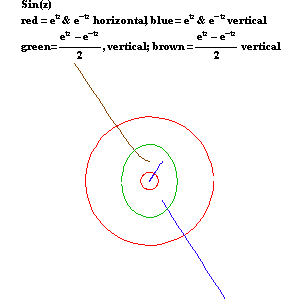The Dramatic Power of Abelian Functions
To understand Riemann’s treatment of Abelian functions, situate that discovery within the context of the history in which it arose, reaching back to the pre-Euclidean Pythagoreans of ancient Greece, and forward to LaRouche’s unique and revolutionary discoveries in the science of physical economy. Imagine that entire sequence, all at once, as a dramatic history, leap over time, project the past into the future, the future into the past, and both into the present, so that centuries of accomplishment are telescoped into a single, instantaneous thought.
Dynamis
In the opening scene of Plato’s {Theatetus} dialogue, Euclides of Megara informs Terpsion that he has just seen Theatetus being carried to Athens, near death, after being wounded in the battle at Corinth. This experience prompts Euclides to recall that Socrates, when near his own death many years before, had told him that “Theatetus will be a remarkable man if he lives.” Now, contemplating Theatetus’s life at its end, Euclides reports that Socrates had also recounted his first conversation with Theatetus when the latter was merely a boy. Having written down Socrates’s report, Euclides now reads the history to Terpsion, the which forms the bulk of Plato’s dialogue. As Euclides tells it, the conversation began with the young Theatetus being praised by his teacher Theodorus, because the former had surpassed the insights of the latter. As Theatetus explained, Theodorus had taught him about the incommensurablity of lines that double, triple, quintuple, etc. a square, by demonstrating each as a separate and distinct power, beginning with tripling and ending with seventeen, where, “for some reason he stopped.” But, Theatetus continued, “Since the number of powers are innumerable, the notion occurred to us of including them all under one name or species.”
Then by reference to a simple geometrical construction, Theatetus indicates the existence of three distinct {species} of powers: those that generate lines, those that generate squares and those that generate solids. Each species comprises an entire manifold of separate and distinct individual powers. But, each manifold, Theatetus explains, can be thought of under a single principle: linear, quadratic, or cubic.
Not mentioned directly in the dialogue, but prominent in the background, is the related discovery of Archytas, who showed that each species is associated with a different type of physical action: linear, circular and toroidal, respectively.
These discoveries of Theatetus and Archytas demonstrate a power of the mind that the Eleatics, Sophists and later, Aristotle, denied existed, and one that is essential to Riemann’s treatment of Abelian functions: {the capacity of the mind to rise above the finite determinations of sensible objects, and to recognize the higher universal principles that determine them}.
As Theatetus demonstrated, it is possible to {know} an entire species of powers, without having to construct each one individually, by knowing the principle that determines what each individual power can do e.g., double a square– and what they can’t– double a cube. To know that all these individual powers are of one species, {and} that the principle that generates square powers can never generate cubic ones, requires the mind to rise above the characteristics unique to each individual magnitude and recognize the nature of the entire species, {and} the nature of its boundaries.
Aristotle insisted that the human mind did not have this power because, being limited and mortal, it could not rise from finite determinations to universal ones:
“Some, as the Pythagoreans and Plato, make the infinite a principle in the sense of a self- subsistent substance, and not as a mere attribute of some other thing. Only the Pythagoreans place the infinite among the objects of sense (they do not regard number as separable from these), and assert that what is outside the heaven is infinite. Plato, on the other hand, holds that there is no body outside (the Forms are not outside because they are nowhere), yet that the infinite is present not only in the objects of sense but in the Forms also….”
“It is plain, too that the infinite cannot be an actual thing and a substance and a principle….
“Thus the view of those who speak after the manner of the Pythagoreans is absurd….
“This discussion, however, involves the more general question, whether the infinite can be present in mathematical objects and things which are intelligible and do not have extension, as well as among sensible objects. Our inquiry (as physicists) is limited to its special subject matter, the objects of sense, and we have to ask whether there is, or is not, among them a body which is infinite in the direction of increase.” (Physics, Book 5)
Aristotle’s argument is pure sophistry. By {defining} physics to concern only sensible objects, he excludes all consideration of the universal principles that generate those objects. Once excluded, he asserts that such principles play no role in the physical world, because being infinite, they cannot actually exist.
Contrary to Aristotle, as Theatetus demonstrates, in and through Plato’s dialogue, or as Socrates himself makes clear in numerous other locations, most notably the {Phaedo}, immortality, not temporal boundaries, characterizes the human spirit. It can freely transcend the finite limits of the sensual domain through its power to comprehend, not only things, such as lines, squares and cubes, but the powers that generate them. It can transform itself, as Theatetus had shown, from comprehending different powers individually, as Theodorus had taught, to comprehending the concept of an entire species of innumerable individual powers, as he had discovered.
And, as the above account of Plato’s account, of Euclides’s account, of Socrates’ account, of Theatetus’s account of his own discovery illustrates, the human spirit is not constrained by the mortal life in which it originates.
Powers that Generate Powers
The method described in the {Theatetus }dialogue is an elementary, but historically and pedagogically important example of the type of thinking that underlies Riemann’s method, elaborated in his {Theory of Abelian Functions}. There Riemann is dealing with the principles that generate higher and higher species of functions, beyond those contemplated by the Pythagoreans, Theodorus, Theatetus, Archytas and Plato. While Riemann is looking back on what was anticipated by these great ancient minds, he does so from the vantage point of the discoveries of Cusa, Kepler, Leibniz, Gauss and Abel. What these later discoverers demonstrated, was that the species of powers indicated by Plato et al., were superceded by a succession of higher species of successively greater power. Riemann, extending Gauss’s concept of the complex domain, created the means to comprehend the higher power that generates this extended class of higher powers. His treatment of Abelian functions gives expression to the quality of mind that can reach beyond the domain of sense perception, transcend what {appears} to be infinite, recognize the existence of new species of transcendental powers, and {generate} them as higher forms of cognition.
To understand Riemann’s elaboration of Abelian functions it is crucial to emphasize the epistemology underlying Cusa’s earlier discovery of a new species of power, by the method that Cusa called {“Learned Ignorance “}.
Cusa discovered that the incommensurability of the curved to the straight, as exemplified by the incommensurability between a circle and its inscribing and circumscribing polygons, indicated the existence of a new species of power, that transcended those named by Plato, et al. Cusa proved, and Leibniz later elaborated, that this new species, which Leibniz called {transcendental}, could generate all lower, {algebraic} powers, whereas the inverse–to generate the transcendental from the algebraic–is impossible.
Like Plato, Cusa recognized that to comprehend these higher species of powers, the mind had to look beyond the boundaries of the domain of sense-perception, to discover the higher powers that govern it from the outside:
“I know that what I see perceptibly does not exist from itself. For just as the sense of sight does not discriminate anything by itself but has its discriminating from a higher power, so too what is perceptible does not exist from itself but exists from a higher power. The Apostle said, “from the creation of the world” because from the visible world as creature we are elevated to the Creator. Therefore, when in seeing what is perceptible I understand that it exists from a higher power (since it is finite, and a finite thing cannot exist from itself; for how could what is finite have set its own limit?), then I can only regard as invisible and eternal this Power from which it exists….” (Actualized-Potential)
Cusa gave his method a mathematical representation, but {not by the formal, logical deductive procedures of Aristotle, or his later followers, Euler, Lagrange, and the bigoted Cauchy}. In Cusa’s mathematical representation, what appears to be mathematically infinite, that is, what is over, or beyond, the finite, (what Cantor would later call the transfinite) indicates the existence of a new power or principle acting on the domain of sense-perception from outside. Thus, pushing finite mathematical expressions to the boundary, and beyond, reveals the characteristics of those sought for, but yet undiscovered, higher powers:
“…when we set out to investigate the Maximum metaphorically, we must leap beyond simple likeness. For since all mathematicals are finite and otherwise could not even be imagined: if we want to use finite things as a way for ascending to the unqualifiedly Maximum, we must first consider finite mathematical figures together with their characteristics and relations. Next, we must apply these relations, in a transformed way, to corresponding infinite mathematical figures. Thirdly, we must thereafter in a still more highly transformed way, apply the relations of these infinite figures to the simple Infinite, which is altogether independent even of all figure. At this point our ignorance will be taught incomprehensibly how we are to think more correctly and truly about the Most High as we grope by means of a metaphor.” (On Learned Ignorance, Book I.)
Cusa elaborated this metaphor extensively. He examined carefully the difference between the finite relations of the point, line, polygon and circle, and their transfinite relations. In the finite, these objects are each distinct, but transformed into their infinite forms, they become congruent, indicating the existence of the higher principle from which their finite relations are unfolded. Thus, the lower, finite forms are bounded (and governed) by the higher, which, from the standpoint of the lower, {appears} to be infinitely far away. Therefore, to know anything about the relationships in the finite, one must view them from the standpoint of the conditions at that seemingly infinite boundary. As we will soon illustrate, this relationship reaches a more developed form in Riemann’s treatment of Abelian functions.
Like Plato, Cusa associated this capacity of the human mind, to reach beyond the boundary of the apparent infinite, and identify new species of numbers as powers, with the immortality of the soul:
“Likewise, the exhibiting of the mind’s immortality can suitably be pursued from a consideration of number. For since mind is a living number, i.e., a number that numbers, and since every number is, in itself, incorruptible (even though number seems variable when it is considered in matter, which is variable), our mind’s number cannot be conceived to be corruptible. How, then, could the author of number [viz., mind] seem to be corruptible? Moreover, no number can deplete the mind’s power of numbering. Hence, since the motion of the heavens is numbered by the mind, and since time is the measure of motion, time will not exhaust the mind’s power. Rather, the mind’s power will continue on as the limit, measure, and determination of all things measurable. The instruments for the motions of the heavens instruments produced by the human mind attest to its not being the case that motion measures mind rather than mind’s measuring motion. Hence, mind seems to enfold by its intellective operation all movement of succession, and mind brings forth from itself rational operations, or rational movement. Thus, mind is the form of moving. Hence, if when anything is dissolved, the dissolution occurs by means of motion, then how could the form of moving be dissolved through motion? Since mind is an intellectual life that moves itself i.e., is a life that gives rise to the life which is its understanding how would it fail to be always alive? How could self-moving motion cease? For mind has life conjoined to it; through this life it is always alive. (By way of illustration: a sphere is always round, by virtue of the circle that is conjoined to it.) If mind’s composition is as the composition of number, which is composed of itself, how would mind be dissolvable into not-mind?…
…thus, he who numbers unfolds and enfolds. Mind is an {image} of Eternity, but time is an {unfolding} of Eternity…”(The Laymen on Mind)
Unlike the heathen Aristotle, for Cusa, the infinite is not outside the universe. What appears to be infinitely far away from the standpoint of sense-perception, is only the boundary marking the transition to the unseen, but efficient, domain of universal physical principles. Those principles reach through that boundary, into the visible domain, determining the characteristics of action within it. The mind, in turn, reaches back, transcending the apparently infinite, and discovering the characteristics of those principles. {Thus, the appearance of the infinite in mathematical expressions, simply indicates the necessity for a transformation of the mind’s idea a transformation that makes a universal principle that had appeared to be inaccessible, known.}
The Physical Generation of Powers
From Cusa, the road to the discovery of those higher species of transcendental powers that are the subject of Riemann’s work, goes through the investigations of Gauss and Abel who were provoked by:
–Kepler’s discovery that the principle of universal gravitation generated planetary orbits that were essentially elliptical, and;
–Leibniz’s determination that these orbits reflected a universal principle of physical least- action expressed by the catenary curve.
In rejecting the Aristotelean formalism of Ptolemy, Copernicus, and Brahe, and basing his investigation only on physical considerations, Kepler was compelled to reject the mathematically simpler circular orbits for the physically determined elliptical ones. This produced a crisis, because, whereas in a circular orbit, there is an incommensurability between the angle and the sine, in an elliptical orbit, there is an incommensurability between the arc and the angle as well. Kepler’s attempts to measure elliptical motion from the standpoint of the circular functions (i.e., as the connected action of a rectilinear triangle and a circular arc), produced the paradox known as “The Kepler Problem”. Kepler developed a method to approximate this measurement for practical purposes but, for him, this was insufficient. Kepler was not a pragmatist. Though practical solutions were vital to his work, Kepler was insistent on knowing the principle as well. When knowledge of that principle eluded him, Kepler demanded that future geometers solve the problem, insuring that even his own death would not end his quest.
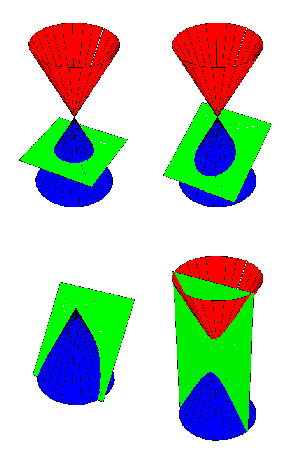
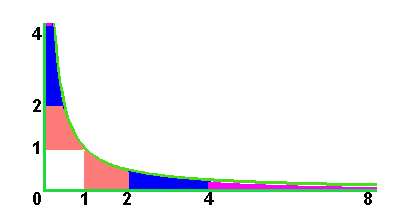
While Kepler did not discover the higher principle of elliptical motion, he indicated where to look. In his related work on optics, Kepler proposed to look at the ellipse as merely one phase in a single function that generated all the conic sections. He expressed this geometrically through his famous projection that carried the circle into a hyperbola. (See Figure 1.) The emergence of an apparently infinite boundary between the ellipse and the hyperbola, within an otherwise continuous function, indicated the direction in which this undiscovered principle could be found.
|
Figure 1 |
The appearance of the infinite boundary between the ellipse and the hyperbola reflects, of course, the double cone construction of the conic section. On one side of the “infinite”, the circle, ellipse and parabola, only the lower cone is cut by an intersecting plane. It is when that plane touches the upper cone, that the hyperbola is formed. (See Figure 2.)
|
Figure 2 |
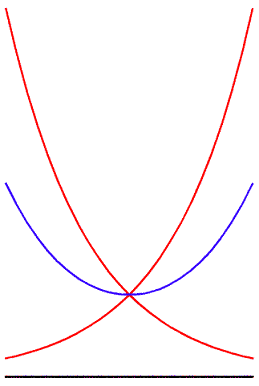
Leibniz, through an application of his infinitesimal calculus, showed that the curvature of the hanging chain can be expressed as the arithmetic mean between two exponential curves. (See Figure 3.) These exponential curves do not exist in the perceptible domain of the hanging chain. Nevertheless, they express a characteristic of the {physical manifold} that is acting, from outside the domain of sense-perception, on the chain, in every infinitesimal interval.
|
Figure 3 |
As Leibniz emphasized, these exponential curves express that transcendental species of power that generates all the lower algebraic ones. (See Figure 4.)
|
Figure 4 |
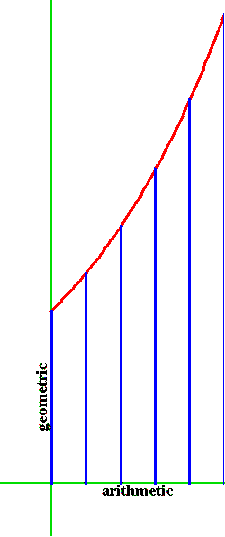
This same relationship is also expressed, in different forms, by the equiangular spiral and the hyperbola. (See Figure 5a, and Figure 5b.)
|
Figure 5a |
|
Figure 5b |
In connection with this investigation of the catenary, Leibniz coined the term {“function”} to denote a specified transformation. So, for example, the exponential function transforms arithmetic relations into the geometric ones. Its inverse, the logarithmic function, transforms geometric relations into arithmetic ones. As the arithmetic mean between two exponential functions, the catenary, therefore, is a function of two functions.
When Leibniz pushed this investigation to its boundary, by attempting to determine the function that generates the logarithms of negative numbers, he met the appearance of the square root of -1, which he identified as existing in a real, but “imaginary” domain.
That Undiscovered Country
Thus, the young Gauss, confronted with the appearance of what Leibniz called, “a fine and wonderful recourse to the divine spirit, almost an amphibian somewhere between being and non-being”, granted the square roots of negative numbers their “full civil rights”. From this standpoint he reexamined the “Kepler Problem”, and discovered that elliptical motion was governed by a higher species of transcendental, that had been anticipated by, but not known to Kepler or Leibniz.
The physical significance of complex numbers emerged quite naturally from Leibniz’s catenary principle and the paradox of negative logarithms. (See Figure 6.)
|
Figure 6 |
Since the catenary is formed as the arithmetic mean between {two} exponential curves, Leibniz sought the function that generated both, which could be expressed as that which generated their geometric mean. But, there is no continuous transformation, within the plane of the catenary, and the exponentials hanging behind it, that can transform one exponential into the other. The only physical action that has the power to produce both curves, is a rotation orthogonal to the plane of the catenary. (See Figure 7.)
|
Figure 7 |
If the direction of one exponential is designated as positive and the other direction negative, the geometric mean between them is expressed as the square root of a negative number. (See Figure 8.)
|
Figure 8 |
This gives rise to the following paradox: In the plane of the two exponentials, the geometric mean between them is a straight-line. But, when looked at from the higher standpoint of physical action, that straight-line is actually the axis of rotation from which is generated an entire surface orthogonal to the plane of the chain. Thus, to represent the physical action of the chain, the unseen exponentials that hang behind it, and the unseen principle that generates the exponentials themselves, requires both the plane of the chain, and the plane of the action orthogonal to it.
Gauss conceived the idea of representing this complex domain on one surface. That surface acts as a stage for the imagination on which {both} the physical action and the universal principles that govern it can be represented.
The two exponentials in the plane of the catenary are generated by an action that is completely outside their visible domain. The point at which the axis of rotation touches the surface generated by that rotation, i.e. the center of the circle formed by that rotation, is the only intersection between the visible domain and the surface on which the principle of generation is represented.
Just as on the Classical stage, a single line, (“Its Greek to me.”) in the context of the drama, can indicate an historical transformation of an entire culture, on the surface representing the complex domain, an entire principle, in the context of a complex function, can be represented by the action at a single point.
Hidden Harmonies Become Heard
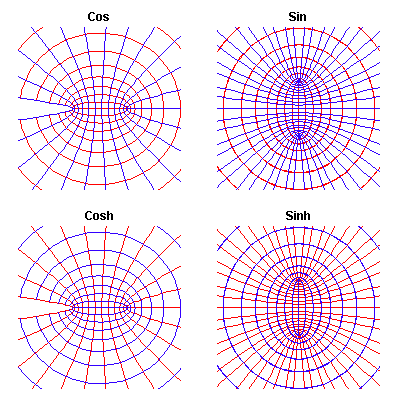
By adopting Gauss’s approach, Riemann was able to create a stage, on which an innumerable class of transcendentals of successively higher power could be brought within the scope of the imagination. Each new species of transcendental, beginning with the simplest species of transcendentals discovered by Cusa, to the elliptical functions of Gauss, to those higher species discovered by Abel, is distinguished from its predecessor by the addition of a new principle. Under Riemann’s idea, each new principle is represented by a change in the geometrical characteristics, {the topology} of the surface.
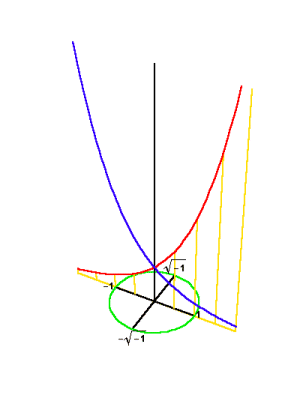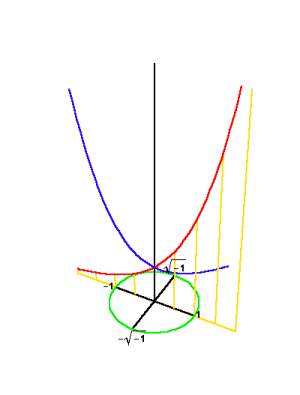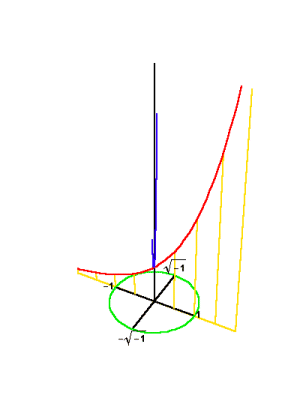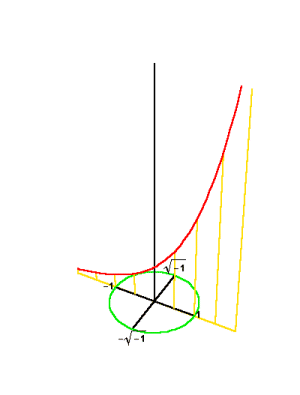
Here Riemann adopted Leibniz’s method of {analysis situs} as applied by Gauss in his 1799 dissertation on the fundamental theorem of algebra. Gauss showed that formal algebra could not distinguish the implications of a change from one power to another. This is reflected, as Gauss ironically emphasized, in the inability, from the standpoint of formal algebra, to answer algebra’s most important question: “How many solutions are there for a given algebraic expression?” It was only when these expressions were thought of geometrically, as surfaces, that their essential characteristics could be made known. Then, it was clear, that the highest power of the function determined a topological characteristic (the number of “humps”) that was independent of any variations in the lower powers or the coefficients of that function. (See Figure 9a, and Figure 9b.)
|
Figure 9a |
Figure 9b |
Thus, Gauss’s employment of Leibniz’s geometry of position, {analysis situs}, expressed the epistemological relationship that the principle associated with the highest power dominated all lower ones. A change in the degree of power is, therefore, a change in the governing principle, and is expressed by a transformation of the entire geometry of the surface. Thus, the essential characteristics of an entire species of algebraic functions could be known completely, without the useless formal calculations of Euler, Lagrange and D’Alembert.
To illustrate Riemann’s approach, we begin with a look at the simplest species of transcendental, those associated with the circular, hyperbolic and exponential functions. As Leibniz and Bernoulli demonstrated the catenary, expressing the universal physical principle of least-action, embodied all three of these functions in one single physical action.
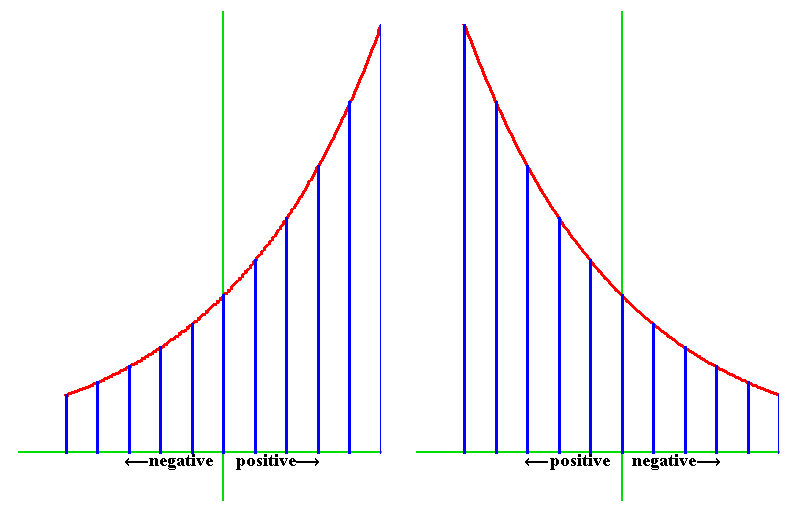
However, from the standpoint of the “simple” domain, these three functions seemed to have entirely different characteristics. For example, the circle and the hyperbola are conic sections, the exponential is not. In the visible domain, the circle is periodic, the hyperbola and exponential appear infinitely extended.
Leibniz imagined that a higher principle united all three transcendentals, but he never elaborated his idea. The sophisticated, but Leibniz-hating Euler, tried to obscure Leibniz’s insight with a series of algebraic formalisms, (such as his infamous equations: ei*Pi-1=0; and ei*x=cos[x]+i*sin[x]) which have bedeviled generations of students and scientists to this day.
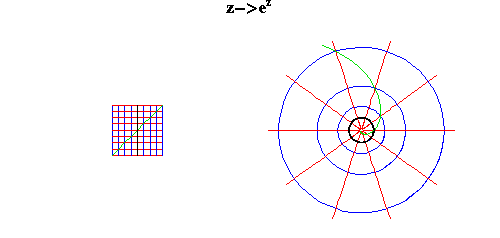
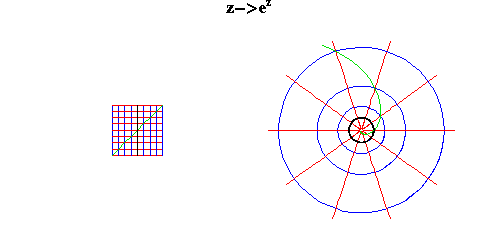
Yet through Gauss’s and Riemann’s physical conception of the complex domain it can be easily demonstrated that these three functions express one unified species of transcendentals, and are all derived from the complex exponential. Gauss recognized this as early as August 14, 1796, writing in his notebook: “By the way, (a+b*?-1)m+n*?-1 has been explained”.
Here Gauss indicates he has extended the idea of the exponential function to the complex domain. As noted above, the exponential function is the transformation of arithmetic relationships into geometric ones. In the “simple” domain, this appears geometrically as the characteristic curvature of a single curve, as, for example, the equiangular spiral, hyperbola or exponential curve. In Gauss’s complex domain, the complex exponential function transforms the arithmetic relations of an entire surface into geometric ones, transforming all curves into new ones.
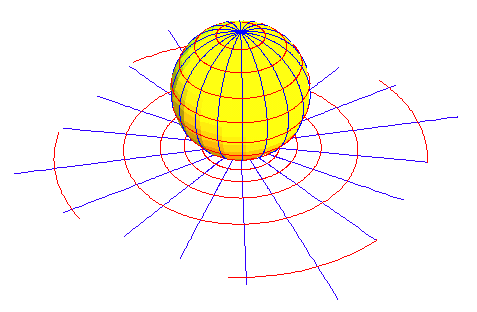
This can be seen most easily from the geometrical example in Gauss’s Copenhagen Prize Essay on conformal mapping (on which Riemann relied.). There Gauss shows that the complex exponential function corresponds to the stereographic projection of a sphere onto a plane a projection first developed by the ancient Greeks in connection with the mapping of the celestial sphere. (See Figure 10.)
|
Figure 10 |
Under this projection, the circles of “latitude” on the sphere are projected onto concentric circles on the plane, whose radii are expanding exponentially. Circles of “longitude” on the sphere are transformed into radial lines on the plane.
Don’t think of this transformation as a static image. Think of it from the standpoint of physical action. Think of the motion along a circle of latitude on the sphere. What is the corresponding motion on the plane? Think of the motion along a circle of longitude on the sphere. What is the corresponding motion in the plane? Think of motion along a path of equal heading on the sphere (loxodrome). What is the corresponding motion along in the plane? When you think of it in this way, you can begin to see how all relationships on the sphere are transformed, lawfully, into different relationships on the plane.
Here a crucial new idea emerges that cannot be seen in the “simple” domain. What appeared to be “infinitely” long radial lines of the plane, become “finite” circles of longitude on the sphere. Action on the plane that appears to go off into the “infinite” approaches a single point on the sphere. From the standpoint of Cusa, if the terminus of all the radial lines in the plane is thought of as the “infinite” circle, its image is a single point on the sphere. In other words, the principle bounding the action on the plane, that appears to be infinite and unknowable, is brought into the imagination, by the action associated with a single point on the sphere. Thus, in the complex domain, we can faithfully represent Cusa’s notion that in the infinite, the center and circumference, minimum and maximum, coincide.
It is important to emphasize, however, that physical action, such as the hanging chain, is never “infinite”. The catenary is the curve of a chain hanging between two positions. Thus, “this side of the infinite”, the physical exponential is always bounded. It is the universal principle that it reflects that is {transfinite}.
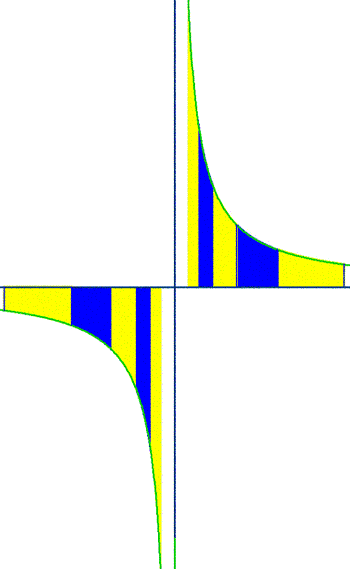
Another characteristic now comes into view that otherwise remained hidden with the “simple” view of the exponential. In the simple domain, the exponential curve appears aperiodic But, this is only an illusion caused by viewing the exponential too simply. As can be seen in the image of the stereographic projection, the radial lines are unbounded, but the circles of latitude are periodic. (As you can imagine, this period is real. It is Euler’s fraud to insist that the period of the complex exponential is “imaginary”.)
The hidden periodicity of the complex exponential can be seen more dramatically when viewed as a transformation of an orthogonal grid of curves on a plane, or, as Riemann suggested, on the surface of a very large sphere. (See Figure 11.)
|
Figure 11 |
Here all “straight” lines are transformed into a network of equiangular spirals, bounded by spirals with maximum rotation and minimum extension (i.e., circles), and spirals with maximum extension and minimum rotation (i.e., radial lines).
Think of this image from the standpoint of action. Under the transformation of the complex exponential, motion along a “straight”line is transformed into spiral motion, including the extreme cases of the circles and the radial lines. The non-periodic motion along the vertical lines is transformed into periodic circular action. (See Figure 12.)
|
Figure 12 |
The aperiodic motion along horizontal lines is transformed into motion along the exponentially extending radii, which remains aperiodic. Motion along a diagonal line is transformed into ever expanding spiral action. (See Figure 13.)
|
Figure 13 |
Now compare this result with what was noted above concerning the two exponential curves associated with the hanging chain. In the visible domain, this action is aperiodic. However, the rotation orthogonal to the plane of the hanging chain has a periodicity. Here we can recognize the physical reality of the exponential function’s “imaginary” period.
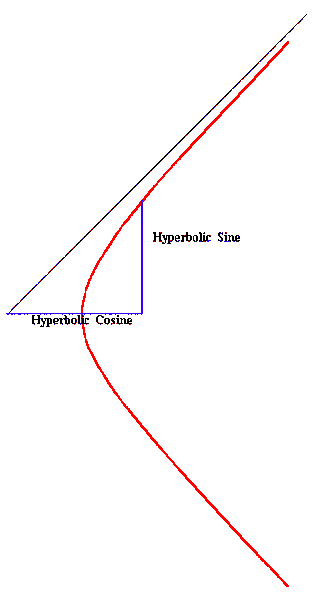
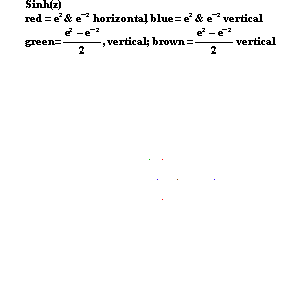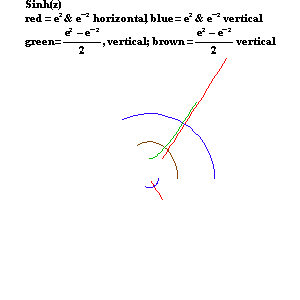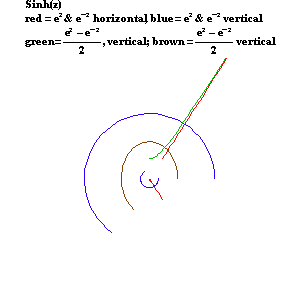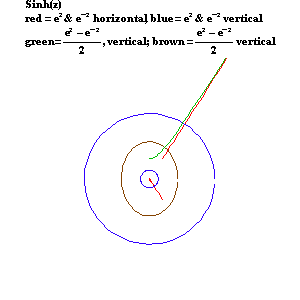
As Leibniz and Bernoulli demonstrated in their work on the catenary, the hyperbolic functions are functions of the exponential: the hyperbolic cosine is one-half the sum of two exponentials and the hyperbolic sine is one-half the difference of two exponentials. (See Figure 14.)
|
Figure 14 |
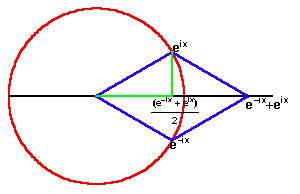
As Leibniz also insisted, the circular functions are also functions of the exponential, but only in a different, “imaginary”, domain. (See Figure 15.) The circular cosine is one-half the sum of two complex exponentials, while the circular sine is one-half the difference of two complex exponentials.
|
Figure 15 |
When viewed from the standpoint of Gauss’s and Riemann’s complex domain, all these functions can be expressed by the same type of action: the arithmetic mean between two complex exponentials moving in opposite directions, as illustrated by the circles in the accompanying animation. (See Figure 16a, Figure 16b, Figure16c, Figure 16d, and Figure 16e.) Together, the hyperbolic and circular functions form the four different variations of the same type of action. Thus, generated by the same type of action, they are all of the same species of transcendental.
|
Figure 16a |
Figure 16b |
|
Figure 16c |
Figure 16d |
|
Figure 16e |
The Elliptical Transcendentals
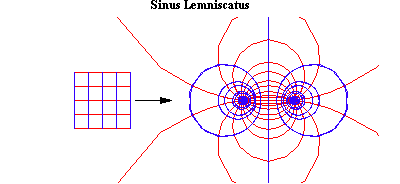
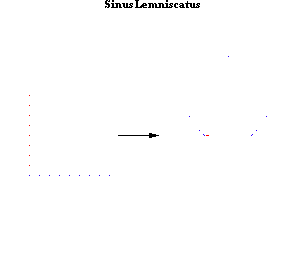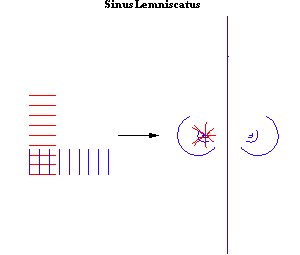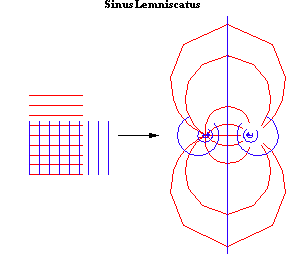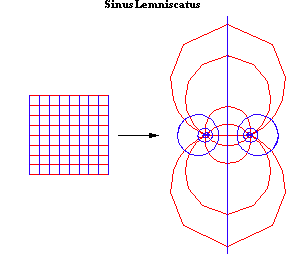
The young Gauss, contemplating the origin of the “Kepler Problem”, was puzzled by the inability to express elliptical motion by the circular, hyperbolic or exponential functions. But, when he looked at a similar problem, that of the lemniscate, from the standpoint of the complex domain, he discovered a different species of transcendental that was expressed by elliptical motion. When the characteristics of that species are viewed on Riemann’s stage, the difference between the elliptical and the lower transcendentals becomes obvious.
While Gauss did not state it this way directly, his January 1797 decision to begin serious investigation of the lemnsicate alludes to the clue suggested earlier by Kepler’s concept of the conic sections.
As noted above, Kepler thought of all the conic sections as being generated from one continuous function. The emergence of an infinite boundary, between the ellipse and the hyperbola, reflects the transition to the inclusion of the upper cone in the double conical function. Thus, the entire function involves action in two different directions (parallel and perpendicular to the base of the cones). When thought of from the standpoint of Cusa, the appearance of the infinite signifies that a higher, undiscovered principle exists that encompasses both the perpendicular and parallel action as one. It is from this higher type of function that Kepler’s conic section function is unfolded.
This function must have the same relationship to the circular and hyperbolic functions as those functions have to the algebraic. That is, the higher species must have the capacity to generate the lower, but not the inverse. This is akin to the relationship between the quadratic and cubic species of magnitudes as viewed from the standpoint of Archytas. The principle of toroidal motion that generates cubic magnitudes can generate the quadratics as well, but not the inverse.
Now what is the nature of these elliptical transcendentals and how can we discover it? Let’s reconstruct Gauss’s investigation of the lemniscate from the standpoint of the clue supplied by Kepler, and the later solution supplied by Riemann.
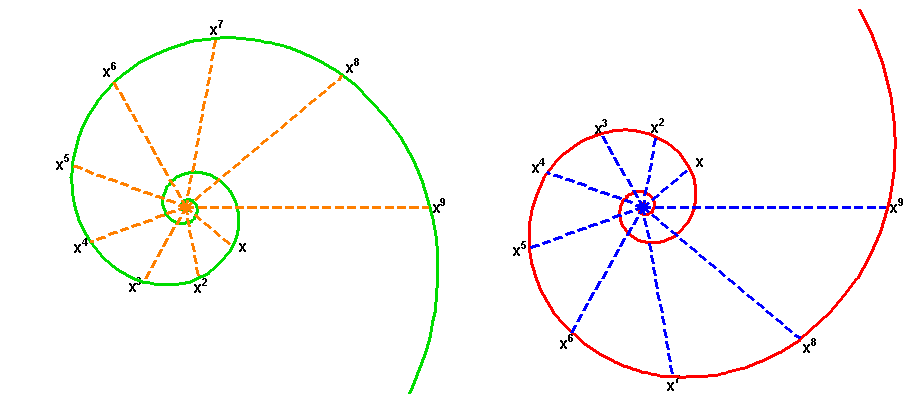
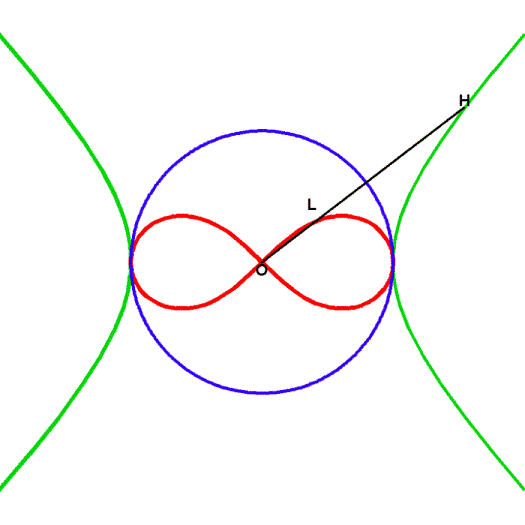
That the lemniscate would become the focus of Gauss’s attention, flows quite naturally from the extension of Kepler’s concept of the conic sections into the complex domain. As presented in previous installments of this series, the lemniscate can be generated as the inversion of the hyperbola in a circle, or the stereographic projection of a hyperbola onto a sphere. (See Figure 17 and Figure 18.) From the standpoint of these two projections, it can be seen that the circle is the geometric mean between the hyperbola and the lemniscate. Thus, we seek a higher function that transforms the hyperbola, through the circle, into the lemnsicate.
|
Figure 17 |
|
Figure 18 |
It is important to take note of the method of inversion employed here. In the case of the two exponential curves and the catenary, the geometric mean between the two exponential curves could not be found within the visible domain of the curves and the hanging chain. The search for the principle that would generate both exponentials led us into the complex domain. In the case of the conic sections, Kepler’s function generates one from the other. But the appearance of the infinite in the middle of the function coaxes us to consider a higher function. That function generates, not another conic section, but a lemnsicate.
Now look at Kepler’s function, as he envisioned it projected onto a plane, and, from Riemann’s standpoint, projected onto a sphere. (See Figure 19.) In the former case, the circle is transformed into an ellipse, which is transformed into an hyperbola, and then into a line. In the latter, the circle is transformed into a projected ellipse, which is transformed into a lemnsicate, and then into two coincidental hemispheric circles.
|
Figure 19 |
Thus, to grasp the higher principle we have to think of both functions happening simultaneously: the one on the stage of the plane that is generating the conic sections, and the one on the stage of the sphere, that is generating a lemniscate. But from our vantage point we see both on {one} stage the stage of the complex domain.
Note that the infinite boundary that appears in the plane, appears in the spherical projection as the crossing point of the lemniscate. This presence of the {transfinite}, represented as a single point in the lemniscate, signifies the existence of an additional principle, that is outside the domain of the conic sections, but, {inside} the domain in which the lemnsicate resides. As noted in a previous installment, Gauss showed that the crossing point on the lemniscate also reflects the boundary between the regions of positive and negative curvature on the torus. (See Figure 20.)
|
Figure 20 |
Does the presence of this new principle indicate that the lemniscate is associated with a different species of transcendental than the circular or hyperbolic functions? Gauss said yes, and Riemann provided the basis to recognize this geometrically.
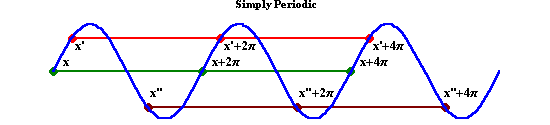
Gauss recognized the existence of this added principle in the lemniscate by the double periodicity of the lemnsicatic functions. Where, for example, the circular functions are periodic with respect to the interval 0 to 2Pi, the lemnsicatic functions are periodic with respect to the interval 1 to -1 {and} the interval /-1 and -/-1. (See Riemann for Anti-Dummies 52.)
Gauss expressed the geometrical characteristic of double periodicity in his work on bi-quadratic residues, which he published in 1832. However, its discovery was much earlier, as indicated by his notebook entry, “I have discovered a remarkable connection between the lemniscate and bi-quadratic residues”.
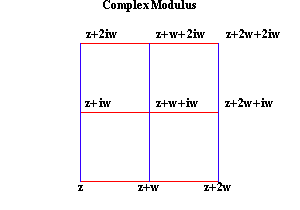
That connection is illustrated by the geometrical representation Gauss gave, with respect to simple and complex moduli, in his {Second Treatise on Bi-Quadratic Residues}. There Gauss shows that for real numbers, the modulus can be expressed geometrically by a simple line segment or curve. (See Figure 21a and, Figure 21b.)
|
Figure 21a |
|
Figure 21b |
However, in the complex domain, a complex modulus is expressed by a parallelogram on a surface. (See Figure 22.)
|
Figure 22 |
This same geometrical distinction, as Gauss noted, also appears in comparing the lemniscate with the circular functions in the complex domain. In the case of the circular, hyperbolic or exponential functions, motion in one direction was periodic, while motion perpendicular to it was not. As illustrated above, this type of motion could be mapped onto a surface such as a sphere.
However, for the lemnsicate, the motion is periodic in two directions simultaneously. (See Figure23a, Figure 23b, and Figure23c.)
|
Figure 23a |
Figure 23b |
|
Figure 23c |
Such motion can not be represented on Riemann’s sphere, where one direction, such as the circles of latitude, are periodic, but, in the orthogonal direction, the circles of longitude, are not periodic without crossing the infinite.
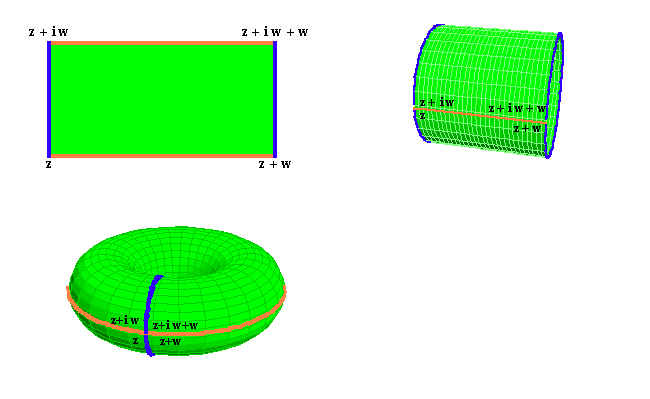
Riemann showed that the elliptical functions could only be expressed on a surface that allowed for two distinct periodic curves. Such a surface can be constructed, Riemann showed, by taking the parallelogram of Gauss’s complex modulus and connecting the opposite sides to each other, forming a surface with the topology of a torus. (See Figure 24.)
|
Figure 24 |
On a torus, there are two distinct curves, one that goes around the outside, and one that goes through the hole. (See Figure 25.)
|
Figure 25 |
Riemann emphasized that the torus is an entirely different type of surface than a sphere. {And, there is no continuous function that can transform a sphere into a torus, without the introduction of a new principle. Once introduced, that new principle effects a complete transformation of all relationships on that surface.}
Through this investigation into the distinction between the higher species of elliptical transcendentals and the lower species, we are able to recognize that the difference between these two species of transcendentals reflects a fundamental change in the number of principles acting through each species. As Abel showed, an entire class of transcendentals can be constructed of successively higher power . In Riemann’s elaboration, the change from one species to the higher, conforms to a transformation from a domain of “n” principles to a domain of “n+1” principles. As in Archytas’s construction for the doubling of the cube, or Gauss’s method of his 1799 dissertation on the fundamental theorem of algebra, such transformations can be made intelligible on the stage of the complex domain, as a discontinuous transformation in the {topology} of that domain.
More importantly, however, armed with this new power to make intelligible the generation of higher species of transcendentals, we can now envision the transformation that must occur, in any domain when a new principle is added. Thus, through the willful employment of the mind’s power of discovery, we can reach past the boundary of what seems to be infinite, and bring new principles into our conscious possession.
And this brings us back to Theatetus, who, as a young boy, shows us today, that an entire species can be known, completely without calculation.