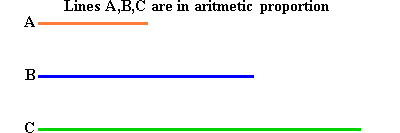Category: Riemann for Anti-Dummies

Riemann for Anti-Dummies Part 44

PRINCIPLES AND POWERS

Rembrandt van Rijn’s masterpiece, ?Aristotle Contemplating a Bust of Homer?, conveys a principle that leads directly into the deeper implications of Gauss’ and Riemann’s complex domain. In the painting, the eyes of both figures are fixed directly before them, yet, Aristotle’s gaze is insufficient to guide him. To find his way, he reaches forward to touch the likeness of the poet, who, though blind in life, leads the blocked philosopher in a direction he would otherwise be incapable of finding.

Like the navigators of ancient maritime civilizations, Rembrandt’s Homer knows that straight-ahead is not necessarily where your eyes point. When following a course across some wide expanse, these discoverers would mark their passage by noting the motions of celestial bodies, the which were charted as changes of positions on the inside of the sphere whose center was the eyes of the observer. When the observer’s position changed, so did the positions of everything on the sphere, but the manifold of vision remained a sphere and the eyes of the observer remained at its center. A stationary observer would note certain changes in the positions of celestial bodies over the course of a night and from night to night. An observer moving on the Earth noted these changes, plus the changes in these changes resulting from his own motion. These changes, and changes of changes, formed a map in the mind of the explorer — not a static map, but a map of the principles that caused the map to change. It is the map of principles on which all explorers, from those days to this, place their trust.

While a map, such as one of positions of celestial bodies on the inside of a sphere, can be represented directly to our senses, a map of principles can only be represented by the methods exemplified by Rembrandt’s painting. Principles do not appear as objects in the picture, but as ironies that evoke the formation of their corresponding ideas in the imagination of the viewer. The scientist in pursuit of unknown principles, must master the art of recognizing the ironies that appear, not only from known principles, but those still to be discovered; the latter emerging as paradoxes. In the case of physical principles investigated by mathematical images, these paradoxes present themselves as anomalies, as for example, the emergence of “-1, within the domain of algebraic equations. The poetic scientist takes the existence of such anomalies as evidence of a principle yet to be discovered, and re-thinks how his map must change to include this new principle. C.F. Gauss measured this type of transformation as a change in curvature. This work was extended by B. Riemann through his theory of complex functions, most notably in his major works on the hypergeometric and abelian functions.

What has failed Rembrandt’s Aristotle, is not his eyes, but his map. A map which has changed by a principle, that on principle, he insists doesn’t exist and cannot be known if it did. Disoriented he’s left to grope in the only direction he knows straight ahead. Fortunately for him, straight ahead stands the lifeless image of Homer, possessed with the power to light his way.

Curvature and Power

This method of discovery is already evident in the work of Archytas, who taught that the physics of the universe could be discovered through investigations of the paradoxes arising in arithmetic, geometry, spheric (astronomy) and music. His collaborator, Plato, prescribed mastery of these four branches of one science, as essential for the development of political leadership.

The solution Archytas provided for doubling the cube exemplifies the principle. As it was developed more fully in previous pedagogical discussions (see Riemann for Anti-Dummies Part 42) the problems of doubling the line, square and cube, presents us with the existence of magnitudes of successively higher powers, each of which is associated with a distinct principle. The Pythagoreans called the power that doubles the line, arithmetic, and the power that doubles the square geometric, which they associated with musical intervals as well as mathematical ones. In their most general form, the arithmetic is associated with a division of a line, while the geometric is associated with a division of a circle. (See figure 1 and figure 2). From Gauss’ standpoint, the change in power from the arithmetic to geometric is associated with a change in curvature from rectilinear to circular.

Figure 1

Figure 2

As Hippocrates of Cios indicated, to double the cube requires placing two geometric means between two extremes. At first blush, this can be accomplished within the domain of circular action by connecting two circles to each other. (See figure 3.) Thus, while the difference between the arithmetic and geometric presents clearly a change in curvature, the power associated with generating two geometric means, in first approximation, seems to require only another circle, hence, no change in curvature.

Figure 3

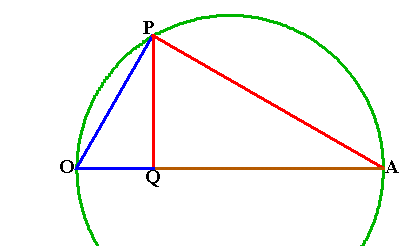
Yet, when the specific physical problem of doubling the cube is posed, that is, to find two geometric means between two determined extremes, (in this case 1 and 2) the existence of the higher power emerges into the map, as a new type of curvature. (See animation 1.) As can be seen in the diagram, to find two geometric means between 1 and 2, we must find the place along the circumference of the circle for point P so that the line OB is one-half of OA. This will occur somewhere along the pathway traveled by B as P moves around the circle from O to A. But, as the dotted line which traces that path indicates, this curve is not a circular arc, and is, in fact, non-uniform with respect to the circle. Thus, the existence of the yet to be discovered principle, emerges through the presence of an anomalous change in curvature in our map.

Animation 1

This anomaly takes on an entirely different characteristic in Archytas’ construction using the torus, cylinder and cone. (See figure 4 andanimation 2.) When the torus and cylinder are generated by rotating one circle orthogonally around another, the motion of point P is now simultaneously on two different curves: the circle and the curve formed by the intersection of the torus and the cylinder. An observer facing the rotating circle, and who was rotating at exactly the same speed as the circle, would only see point P move around the circumference of the circle and would adequately conclude that one geometric mean between two extremes is a function of circular action alone. But, as indicated above, the emergence of the non-circular curvature of the path of point B, would indicate to such an observer, the existence of a new principle causing the motion of P around the circle. Archytas’ construction takes that new principle into account, by determining the motion of P around the circle as a function of P’s motion along the curve formed by the intersection of the torus and cylinder. In other words, the circular rotation of P is only a shadow of a higher form of curvature. That latter curve expresses both the power to produce one geometric mean between two extremes, and also, when combined with a cone, to produce two. (See figure 4.)

Figure 4

Animation 2

Two other examples, presented summarily, will help illustrate the point. Kepler, like all astronomers before and since, observed the motions of the planets as circular arcs on the inside of a sphere. His discovery of the elliptical nature of these orbits occurred, not by suddenly seeing an ellipse, but by his recognition that the 8′ of an arc deviation between the circular image of the planet’s orbit on the celestial sphere, and the circular image of the Earth’s motion (as reflected in the motion of the fixed stars on that same celestial sphere), was evidence of a new principle of planetary motion. The new principle manifested itself as a change in curvature within his map of principles. He measured that change in curvature by measuring equal areas instead of equal arcs, and measuring eccentricities by the proportions that correspond to musical harmonics.

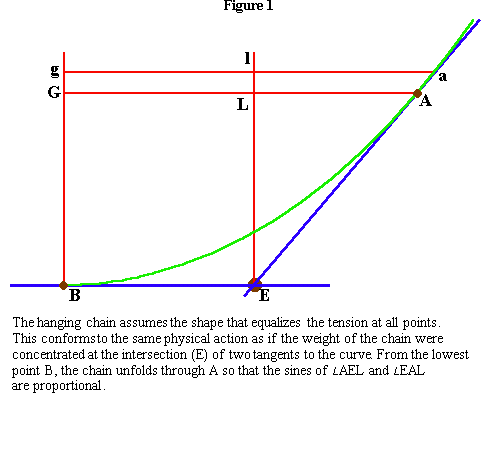
Similarly, Leibniz and Bernoulli determined that the catenary was not the parabola that Gallileo wrongly considered it to be, by showing that the slight deviation of the curvature of the physical hanging chain, from the curvature of the parabola, was evidence that the chain was being governed by a different principle than the one Gallileo assumed. Gallileo demanded, as if in a bi-polar rage, that the chain conform to a parabolic shape, because he was obsessed with his mathematical formula that the velocity of a falling body varies according to the square root of distance fallen. Leibniz and Bernoulli, demonstrated that the chain was, in truth, obeying a higher principle, the non-algebraic, transcendental principle associated with Leibniz’ discovery of natural logarithms. A principle that the enraged Gallileo was incapable of conceiving.

Gaussian Curvature

To proceed further it is important to distinguish between commonplace sense-certainty notions of curvature and the rigorous understanding of that idea associated with Gauss. The commonplace notion, associated with the doctrines of Gallileo, Newton, Euler, et al. is that curvature is a deviation from the straight. But, from the standpoint of the planet, for example, ?straight?, is a unique elliptical path; or, from the standpoint of a link in a chain, ?straight? is the catenary curve. It is only a self-deluded fool who thinks that ?straight? can be determined by some arbitrary, abstract dictate. Rather, ?straight? is a function of the set of principles that are determining the action. The addition of a new principle will change the direction of ?straight?. That change in principle is measured as a change in curvature.

This is the basis from which Gauss developed his, ?General Investigations of Curved Surfaces?. He considered a curved surface to be a set of invariable principles that determined the nature of action on that surface. As long as that set of principles was not changed, the nature of the action did not change, even if the surface was bent or stretched. The nature of the action could only be changed, by a change in the set of principles that defined the surface. Gauss measured such a change in principle as a change in curvature, which in turn, determined what is ?straight? with respect to that set of principles.

Furthermore, Gauss showed, as Leibniz did for curves, that this set of invariable principles were expressed in the smallest elements of the surface. Consequently, from the smallest pieces of ?straight? curves (geodesics) on the surface, and their directions, the curvature of the surface could be determined. (This aspect of Gauss’ work will be developed in a future pedagogical.)

The method Gauss developed to measure curvature had its roots in Kepler’s method for measuring the elliptical nature of a planetary orbit, the which was generalized by Leibniz into his development of the calculus. Confronting the difficulty of measuring the planet’s non-uniform elliptical motion directly, Kepler mapped the constantly changing speed and direction of the planet onto a circular path, and measured the planet’s action by the relationships among the three anomalies (eccentric, mean and true) that appeared in the circular map. (See Summer 1998 Fidelio pp. 29-34).

To measure the curvature of a surface, Gauss extended Kepler’s method from the mapping of a curve onto a circle, to the mapping of a surface onto a sphere, a method he likened to the ancient use of the celestial sphere in astronomy. In that case, the motion of celestial bodies are mapped by the changing directions of lines from the observer to the body’s image on the inside of the celestial sphere. Since whatever principle is governing the body’s motion, is governing the changes in direction of those lines, measuring the map of those changes in direction is an indirect measurement of the governing principle.

Gauss recognized that the invariable principles governing a surface could be expressed by the changing direction of the lines perpendicular to the surface at every point, called ?normals?. While at any point of a surface there are an infinite number of tangents (See Figure 4) there is a unique tangent plane for each point, which in turn defines a unique normal that is perpendicular direction to this tangent plane. The direction of the normal is a function of the curvature of the surface. (This is a principle of physical geometry, as exemplified by the determination of the physical horizon as that direction that is perpendicular to the pull of gravity.)

The sphere has the unique characteristic that all its normals are also radial lines. Using this property, every normal to a surface will correspond to a radial line of a sphere that is pointing in the same direction. As a normal moves around on a surface, its direction changes. If a radial line of the sphere is made to change its direction in the same way as the normal to the surface, it will trace out a curve on the surface of the sphere, that will reflect the principle governing the changes in direction of the normal on the surface.

This is illustrated by example in animation 3 and animation 4. In these examples, the part of the ellipsoid marked out by the yellow curve, is mapped onto a sphere. As the red stick moves around the ellipsoid, its changing direction is determined by the changing curvature of the surface. These changes are mapped onto a sphere, by the motion of the blue stick, which emanates from the center of the sphere and is always pointing in the same direction as the red stick. Gauss called the area marked out by the blue stick on the sphere the, ?total or integral curvature? of the surface. If the red stick were moving along a plane, its direction would not change, and the blue stick would not move. Since this would obviously mark out no area, Gauss defined a plane as a surface of zero curvature. The greater the area marked out on the sphere, the greater the curvature of the surface being mapped.

Animation 3

Animation 4

This can be seen from the above two examples. In animation 3 the red stick is moving around a large area of the ellipsoid, but because that region is less curved, its direction doesn’t change very much, and the corresponding area on the sphere is small. Whereas, in animation 4, the area on the ellipsoid is small, but very curved, so the area marked out on the sphere is larger.

This total curvature does not change even if the surface is deformed. For example, try and determine the spherical map of a part of a cone or a cylinder.

Using this method, Gauss was able to not only measure the ?amount? of curvature, but he was also able to distinguish types of curvature that are determined by different sets of principles. For example, animation 5 illustrates the mapping of a surface called a ?monkey saddle?. (This type of surface should be familiar to those who have been working on Gauss’ 1799 proof of the fundamental theorem of algebra.) In this mapping the curvature of the area denoted by the yellow curve on the monkey saddle is mapped to the sphere. As the red stick moves once around the area on the monkey saddle, the blue stick marks out the spherical area twice. This double covering of the spherical area indicates that the curvature of the monkey saddle embodies a different set of principles than the curvature of the ellipsoid.

Animation 5

A still different type of curvature emerges when Gauss’ mapping is applied to a torus as in animation 6, and animation 7. In animation 6, a part of the outside of the torus is mapped producing a corresponding area on the sphere, similar to what happened on the ellipsoid. But, in animation 7, the area of the torus is situated on both the inner and outer part. The mapping of these directions produces a figure eight type of curve on the sphere that crosses itself at the north pole. Each time the red stick crosses the circle that forms the boundary between the inner and outer part of the torus, the blue stick crosses the north pole of the sphere, with one loop of the figure eight corresponding to the inner part of torus, and the other loop the outer part. The area on the torus is bounded by a non-intersecting curve, while its map on the sphere is bounded by an intersecting one. The presence of this singularity on the spherical map indicates that the boundary between the inner and outer parts of the torus is a transition from one type of curvature to another. Consequently, the torus must be governed by a different set of principles than the ellipsoid or monkey saddle a set of principles that encompass a transition between two different types of curvature.

Animation 6

Animation 7

To summarize: for the ellipsoid, the Gaussian mapping produced a simple area whose size varied with the curvature of the surface. The mapping of the monkey saddle produced an area that was double covered. The mapping of the torus, produced a singularity. These mappings not only measure the ?amount? of total curvature of the part of the surface mapped, but the appearance of anomalies and singularities in the mapping, indicate the presence of additional principles of curvature as well.

Like the Chorus in Shakespeare’s Henry V, who, alone on an empty stage, summons the imagination of the audience to envision the real principles of history and statecraft that are to be depicted, these anomalies and singularities call the attention of the scientist to imagine the set of principles that produced them. Therein, is where

Riemann for Anti-Dummies Part 42

ARCHYTAS FROM THE STANDPOINT OF CUSA, GAUSS, AND RIEMANN

A citizen in 2003 A.D., wishing to muster the conceptual power necessary to comprehend today’s historical, political and economic crisis, and to act to change it, will find it of great benefit to bind into one thought, Archytas’ construction for finding two mean proportionals between two extremes, (circa 400 B.C.), with Bernhard Riemann’s 1854 lecture, “On the Hypothesis which Underlie the Foundations of Geometry”. Two thoughts, separated temporally by 2400 years, recreated simultaneously by one mind yours.

The summary of the relevant concept, spoken by the then 28 year old Riemann acting under the tutelage of the 77 year old C.F. Gauss, focuses on the relationship of the idea to that which creates it:

“Accordingly, I have proposed to myself at first the problem of constructing the concept of a multiply extended magnitude out of general notions of quantity. From this it will result that a multiply extended magnitude is susceptible of various metric relations and that space accordingly constitutes only a particular case of a triply-extended magnitude. A necessary sequel of this is that the propositions of geometry are not derivable from general concepts of quantity, but that those properties by which space is distinguished from other conceivable triply extended magnitudes can be gathered only from experience. There arises from this the problem of searching out the simplest facts by which the metric relations of space can be determined, a problem which in nature of things is not quite definite; for several systems of simple facts can be stated which would suffice for determining the metric relations of space; the most important for present purposes is that laid down for foundations by Euclid. These facts are, like all facts, not necessary but of a merely empirical certainty; they are hypotheses; one may therefore inquire into their probability, which is truly very great within the bounds of observation, and thereafter decide concerning the admissibility of protracting them outside the limits of observation, not only toward the immeasurably large, but also toward the immeasurably small.”

It must be kept in mind, that Archytas, like Riemann and Gauss, was anti-Euclidean. In fact, even Euclid was more anti-Euclidean than today’s neo-Aristotelean followers of Galileo, Newton and Kant, who assert that physical space-time conforms, a-priori, to the axioms, postulates and definitions of Euclidean geometry. No where in Euclid’s Elements is such a preposterous assertion stated. Rather, the Elements are a compilation of earlier discoveries that could never have been produced by the logical deductive methods used in the Elements. The actual method of discovery is best indicated when the Elements are read backwards; from the 13th book on the spherical derivation of the five regular solids, to the 10th book on incommensurables, to the middle books on proportions, to the opening sections on the circular derivation of constructions in a plane.

Archytas’ magnificent composition could only have been produced by a mind closer to Riemann’s than Euclid’s, and, having lived and worked nearly a century earlier, we can be assured that his was not constricted by the deductive method of the Elements, let alone its later Aristotelean transmogrifications. The few extant fragments of Archytas indicate his concept of mathematics was far different from today’s formalists:

“Mathematicians seem to me to have excellent discernment, and it is not at all strange that they should think correctly about the particulars that are; for inasmuch as they can discern excellently about the physics of the universe, they are also likely to have excellent perspective on the particulars that are. Indeed, they have transmitted to us a keen discernment about the velocities of the stars and their risings and settings, and about geometry, arithmetic, astronomy, and, not least of all, music. These seem to be sister sciences, for they concern themselves with the first two related forms of being number and magnitude.”

As with his collaborator Plato, Archytas understood that the betterment of humanity depended on the improvement of the cognitive powers of the mind through pedagogical exercises:

“When mathematical reasoning has been found, it checks political faction and increases concord, for there is no unfair advantage in its presence, and equality reigns. With mathematical reasoning we smooth out differences in our dealings with each other. Through it the poor take from the powerful, and the rich give to the needy, both trusting in it to obtain an equal share.”

However, today’s responsible citizen need not rely merely on fragmentary quotes to bring Archytas’ method into his or her mind. A more secure approach is directly accessible–coming to know for oneself, Archytas’ solution for the problem of doubling the cube a method advocated by Archytas himself:

“To become knowledgeable about things one does not know, one must either learn from others or find out for oneself. Now learning derives from someone else and is foreign, whereas finding out is of and by oneself. Finding out without seeking is difficult and rare, but with seeking it is manageable and easy, though someone who does not know how to seek cannot find.”

The Polyphonic Determination of Mean Proportionals

To begin to obtain knowledge of Archytas’ method, one must throw out all axiomatic/deductive approaches and adopt the physical/geometrical approach demonstrated by Jonathan Tennenbaum in his quite notable pedagogical exercise: “A Note: Why Modern Mathematicians Can’t Understand Archytas” That discussion should be throughly worked through and forms an excellent basis for the pedagogical workshops now taking place among youth organizers and others. That argument is summarized here with the aid of some graphics and animations.

To double the cube, Archytas focused on the more general form of the problem posed by Hippocrates of Cios, that of placing two means between two extremes. Hippocrates had recognized that when doubling the square, the areas of the squares produced, as well as the corresponding sides, were all in what the Pythagoreans called “geometric” proportion. A similar relationship held when doubling cubes, but with one notable exception. Instead of one geometric mean between each action, the cube required two.

For example, if we take a square and double its side, the area of the square so produced quadruples. Thus, the square whose area is double, is the geometric mean between the original square and the square produced by doubling its side. That proportion expressed in numbers is 1:2::2:4. This same proportion is reflected among the sides of the three squares. That is, the side of the square of 1 is to the side of the square of two, as the side of the square of two is to the side of the square of four. Or, in numbers, 1:\/2::\/2:2. Thus, doubling a square amounts to constructing the geometric mean between 1 and 2.

However, when the edge of a cube is doubled, the volume of the cube increases from 1 to 8. From the standpoint of whole numbers, there are two geometric means between 1 and 8, specifically 2 and 4. Hippocrates noted that a similar proportionality exists between the edges of these cubes. The problem, as Riemann would recognize it, is extending this relationship outside the realm of visible observation between 1 and 8, into the smaller interval between 1 and 2. The discrepancy between what can be done in the large and with what can be done in the small, is analogous to the idea of a changing geodesic from the macro-physical to the micro-physical domain, and indicates that the doubling of cube is an action of a higher power, as Plato defines power.

The relationship between the problem of doubling the cube and the problem of finding two geometric means between two extremes, can prove a stubborn one to master for those stuck in logical/deductive habits. The root of this mental block is in large part due to the false, but persistent, habit of trying to understand things from the bottom up. While in the domain of squares, the geometric means from one to eight are created one at a time, one, then two, then four, then eight; in the domain of cubes, these two geometric means, must be created all at once from the top down.

Archytas, who understood music, geometry, number and sphaerics (astronomy) as one, would have no more problem with this than J.S. Bach, Mozart, Beethoven, Schubert, Schumann or Brahms. For the well-tempered system of bel-canto polyphony is not produced from the bottom up, note by note. Rather, each note is determined from the relationships that arise from bel-canto sung polyphony. Thus, think of the placing of two means between two extremes in the same epistemological light as a musical composition. The composer’s idea of the composition determines the relationship among the notes. The question Archytas solved, was, “What composition produces two geometric means between two extremes?”

As demonstrated in the above cited pedagogical discussion by Jonathan Tennenbaum, the placing of one geometric mean is a function of circular rotation, not the generation of squares. While the doubling of the square requires finding the geometric mean between 1 and 2, the circle expresses the placement of a geometric mean between any two extremes. (See figure 1.) In the figure, triangle OPA is inscribed in a semi-circle making the angle at P a right angle.(fn.1.) A line drawn from P perpendicular to diameter at Q, forms a whole set of geometric proportions. The one that most concerns us here is OQ:OP::OP::OA. As P rotates around the circle from A to O, OP remains the geometric mean between OQ and OA, even though the proportion between OQ and OA changes from 1:1 to 1:0.(fn2.) (See animation 1.)

Figure 1

Animation 1

As indicated in Jonathan’s pedagogical, a second set of geometric proportions can be linked to this first set, by drawing a circle around right angle OPQ and finding B as a projection of Q onto OP. (See figure 2.) This produces the double set of geometric proportions OB:OQ::OQ:OP::OP::OA. Now, as P moves from A to O, not only do the geometric relationships between OQ, OP and OA change, but so do the geometric relationships between OQ, OB and OP. (See animation 2.)

Figure 2

Animation 2

Think of these sets of relationships polyphonically. OQ:OP::OP:OA is one voice. OB:OQ::OQ::OP is a second voice. The internal relationships within each voice are the same, but together they form a relationship between two sets of relationships, akin to the voices in a two part fugue.

The problem Archytas confronted is expressed by the non-uniform nature of the curve traced by B as P moves around the larger circle. In order to double the cube, there must be some definite way to determine a ratio between OB and OA of 1:2.

Archytas recognized that this could not be determined in what Riemann called a doubly-extended manifold, but rather, was derived from the higher powers associated with a triply-extended manifold.

Archytas effected this by generating the first set of geometric means from rotating one circle (with diameter AO) perpendicular to another (with diameter OD). (See animation 3.) A point P on circle AO connected perpendicularly to a point Q on the circumference of circle OD, produces the geometric relationship, OQ:OP::OP::OA. The action of the rotating circle AO produces a torus. (See animation 4.)

Animation 3

Animation 4

The rotation of PQ produces a cylinder (See animation 5.) The intersection of the torus and cylinder forms a curve of double curvature, which expresses, from the standpoint of a higher power, the geometric relationships between OQ, OP and OA. Now, when Q is projected to a point B on OP the relationship OB:OQ::OQ:OP::OP:OA is produced. (See Figure 3.)

Animation 5

Figure 3

From this, the magnitude that doubles the cube can be found by constructing OM as a chord of circle OQD so that it is of diameter OD. (See Figure 4.) Rotate chord OM around the axis OD until it coincides with line OP. This action produces a cone with apex at O and axis OD. P now lies at the intersection of a cone, torus and cylinder. After this rotation, M will coincide with B and the length of OB will equal OM. Consequently, if OB=1, OQ is the edge of the cube whose volume is 2; OP is the edge of the cube whose volume is 4; and OA is the edge of the cube whose volume is 8.

Figure 4

The Maximum and Minimum

With the just completed work fresh in mind, step back and ask an elementary question. What universal principle is expressed by the physical characteristic that a doubly extended manifold expresses one geometric mean between two extremes, while a triply extended one requires two? As Plato states in the Timaeus, this is not an abstract question, but one necessary to know in order to understand the real world:

“Now if the body of the One had to come into existence as a plane surface, having no depth, one mean would have sufficed to bind together both itself and its fellow terms; but now it is otherwise; for it behoved it to be solid of shape and what brings solids into unison is never one mean but always two.”

A crucial insight can be gained when this question is examined from the standpoint of Nicholas of Cusa’s principle of the Maximum and Minimum.

Look back at our initial exploration of geometric means. We discovered that this relationship is expressed by a right angle in a circle. But, there was an underlying assumption that we didn’t investigate. What is a right angle? Should we accept some definition, such as Euclid’s, that a right angle is that angle formed when two lines that intersect form two angles that are equal? Should we accept the definition of right angle as that angle inscribed in a semi-circle, when such a definition assumes that the sum of the angles of a triangle equals two right angles? As Kaestner and Gauss would later demonstrate, such definitions already assume that the manifold in which the action occurs is characterized by infinite flatness.

Even before Kaestner and Gauss raised these questions, Cusa recognized that such formal definitions never lead to the truth. For Cusa, the truth is the unqualifiedly Maximum, which, in the Absolute, coincides with the unqualifiedly Minimum.

“Therefore, the truth, which is itself the measure of things, is not comprehensible except through itself. And one sees that in the coincidence of the measure and the measured. Indeed, in everything this side of the infinite, the measure and the measured differ according to more or less. In God, however, they coincide. The coincidence of opposites is therefore like the periphery of the infinite circle. The distance of opposites is as the periphery of the finite polygon. Therefore, in theological figures the complement of that which can be known is to know this, namely, that in the infinite the difference of the measure and the measured is in God equality or coincidence. Hence, the measuring is there infinite rectitude. And the infinite circular line is measurable through infinite rectitude. And the measuring itself is the unity or the connection of both.”

This method of the maximum and minimum is already implicit in the problem addressed by Archytas. The maximum and minimum coincide in God, but “this side of the infinite” they’re opposites. Physical action, can be thought of as least-action, or a mean between the extremes of the minimum and maximum.

As Cusa notes, the circle is generated as the action that encompasses the maximum area by the minimum circumference, otherwise known as “isoperimetric”. This action of circular rotation, itself contains a maximum and minimum. If the rotation begins from a point A, then there is some point O at which the rotating point has reached a maximum divergence from A and begins to converge back towards A. Thus, the circle, which is itself a maximum/minimum, contains within it, another maximum/minimum, expressed by the ends of the diameter as points of maximum divergence.

This principle of maximum divergence within a circle, also contains within it, a maximum and minimum. The angle formed by a line pivoting about the center of the circle reaches an angle of maximum divergence, which now defines a right angle, which Cusa calls the maximum acute angle and the minimum obtuse angle. In other words, instead of defining a right angle as a thing, think of it as a maximum/minimum within a circle, which is itself a maximum/minimum within a doubly-extended manifold. It is here, in the nature of the doubly- extended manifold, that the minimum/maximum characteristics expressed by the circle, and in turn, the right angle, are determined.

Thought of from this standpoint, the geometric mean expresses this maximum/minimum relationship of what Riemann would call a doubly-extended manifold. In sum, the circle expresses the maximum/minimum characteristic of a doubly-extended manifold; the right angle, in turn, expresses the maximum/minimum characteristic of a circle. From Cusa’s standpoint, the geometric mean can be thought of as the mean between the maximum and minimum right angle, (as illustrated in the in the first animation.)

Thought of in this way, the geometric mean is not produced by squares. Rather, the squares are artifacts, generated by the placing of one geometric mean between two extremes, which is the characteristic least action principle of a doubly-extended manifold of zero-curvature.

Now on to the real world of solids as exemplified by cubes. Cubes express two geometric means between two extremes. From the standpoint of Cusa’s maximum/minimum, this relationship must express a mean between the minimum and maximum in what Riemann would call a triply-extended manifold. The expression of the maximum/minimum in a triply- extended manifold is spherical action, which encloses the maximum volume in the minimum surface, and produces two orthogonal degrees of circular action. Each circle expresses a complete set of geometric means. But, the two means that produce solid bodies, such as cubes, are only generated when the spherical action is “unfolded” as in Archytas’ construction.

As in the case of the square, the cube does not produce two means between two extremes. Cubes are artifacts generated when two geometric means are placed between two extremes of spherical action, when that action is “unfolded” as in Archytas’ composition. This is a characteristic least-action principle of a triply-extended manifold.

Figure 4

Kepler’s Orbits and the Catenary

Cusa’s method of maximum/minimum led to a revolution in scientific thinking as typified by Kepler’s determination of the harmonic ordering of planetary motion. The position of any planet within its orbit, Kepler demonstrated, is determined by the minimum and maximum speeds of that orbit. From aphelion the planet increases its speed non-uniformly as determined by the speed it intends to be at when it reaches perihelion, and inversely, from perihelion back to aphelion. Thus, each planet’s orbit is a type of mean between these two extremes. Kepler further showed that these intra-orbital extremes when thought of together, form a set of means, as expressed by the musical harmonic relationships among them.

Similarly for Leibniz’ principle of the catenary. As both he and Bernoulli showed, the catenary unfolds its “orbital” pathway from its lowest point, which is the only point that holds up no chain. From a physical standpoint, the catenary is a mean, a least-action pathway, between the maximum potential force and minimum potential force, which are exerted at right angles to each other. This example will rankle anyone stuck in a Cartesian coordinate system, where the horizontal and vertical axes are straight-lines, and the mean between them is just another straight-line at a 45 degree angle to both. In Leibniz’ physical geometry, the vertical and horizontal are the potential maximum and minimum of physical action, and the catenary is the least action pathway between these two extremes.

Freed, now, from the “ivory tower” notions of Euclidean geometry, as Archytas was, we can gain a greater comprehension of the expression of Cusa’s principle of the maximum/minimum in the Gauss/Riemann complex domain. This is where we’ll begin in the next installment.

FOOTNOTES

1. This should not be taken for granted, and so the reader is encouraged to discover a demonstration that an angle inscribed in a semi-circle is a right angle. The original proof of this is attributed to Thales. The proof in Euclid, III. 31, is based on Euclid’s earlier proof that the sum of the angles of a triangle is equal to two right angles, which Kaestner, Gauss and Riemann would later note depends on the parallel postulate, which in turn depends on an assumption about the nature of the curvature of space. As, Riemann noted in his 1854 habilitation lecture, “these facts are, like all facts, not necessary but of a merely empirical certainty; they are hypotheses;”

2. Here we confront another paradox of abstract mathematics between the expression of the geometric mean in numerical terms, and its physical geometric expression.

DIE WIDMUNG

The following pedagogy is dedicated to the celebration of Lyn and Helga’s silver wedding anniversary on Dec. 29, which is an occasion for joy, not only for said happy couple, but for all people around the world to whom this marriage has contributed such happiness over the past quarter-century.

The Long Life of the Catenary: From Brunelleschi to LaRouche

The shift from a consumer society to a producer one is, fundamentally, a question of understanding power. For consumers, the world is a universe of magical powers, from which the apparent requirements of life are obtained through the intercession of high priests. Such people, when confronted with a turn of events, such as the present, in which the powers on which they’ve relied no longer deliver, become frightened. They demand action from their increasingly impotent priesthood, who, despite all boasts to the contrary, fail to produce results. They then take matters into their own hands, adopting ever increasing desperate rituals designed to appeal directly to the powers on which their hopes are pinned. The high priests, seeking to restore “consumer confidence” and regain their positions of lofty authority, suggest to the frightened populace, that new rituals be performed and new incantations be recited. Each desperate effort fails to bring about any respite from the crisis. Suspicions mount that the unseen potencies have either gone deaf or departed the scene. Dead or deaf, the thought that such powers might never have existed is their ultimate terror. Even if these forces are now believed gone, the idea of their previous existence not only persists, but continues to govern the thoughts and actions of the populari, feeding the hopeless pessimism that leads such unfortunate creatures into a contorted dance reminiscent of those depicted in a Breugel masterpiece.

There was a similar state of affairs in 14th century Florence, when in the aftermath of the Black Death in which nearly 80% of the Florentine population perished, a group of artists succeeded in launching the project to build a Dome with a diameter of 42 meters over the church of Santa Maria del Fiore. (See Figure 1.)

Figure 1

When the decision to undertake that project was made in 1367, the man who would ultimately execute it, Filippo Brunelleshci, was not even born, but the intention that would guide him was already embedded in the proposed size of the structure, and the requirements of its design. The Dome was to be equal in size to the Roman Pantheon, that temple to the mystical powers on whose behalf Roman popular opinion ruled. (See Figure 2a and Figure 2b.)

Figure 2a

Figure 2b

From the time of its construction in 128 A.D. under Emperor Hadrian, the Pantheon had remained the largest domed structure in the world. But, unlike the Pantheon, the Florentine Dome was to be beautiful from both the inside and out. It was to be a complete break with the pantheonic culture that, even though the Emperors had long since ceased to rule directly under its name, had continued to persist for more than 13 centuries and had brought about the very recent calamity from which Europe was still reeling.

The Dome was a project of bold optimism. It would not only span such a large structure, but by being self-supporting and free standing, it would demonstrate a principle that would transform the entire surrounding region, and through the minds of travelers and the imaginations of those with whom they would speak, the entire world.

The full implications of the principles necessary to construct the Dome were not known to the Dome’s original designers, but, to accomplish the feat, Brunelleschi would have to discover, apply, and communicate a form of the universal principle of least-action whose further elaboration would unfold over the ensuing 500 years. The crucial development occurred in 1988, when Lyndon LaRouche, faced with imminent unjust imprisonment, visited the Dome and recognized the implications of Brunelleschi’s discoveries for the subsequent breakthroughs of Leibniz, Gauss and Riemann, and for the future, development of a new physical science.(See 1989 issue of 21st Century with Dome on the cover.)

The Dome and Anti-Euclidean Geometry

Imagine yourself in 1420 looking at the octagonal drum of Santa Maria del Fiore without the Dome. What do you see? Empty space? If so, you would never envision, let alone build, the Dome. The construction of the Dome required a mastery of principles not visible to the eye. Not the invisible mystical powers of the Pantheon, but the universal physical principles, which, though unseen, are known clearly through the imagination. For the scientist, like the artist, there is no empty space, no empty canvass, no blank slate. There is a manifold of physical principles characterized by a set of relationships whose expression takes the ultimate form of the work of art. To visualize the unbuilt Dome, as the artist Brunelleschi would, imagine the physical principles, and the bricks and mortar take the required form.

This is the basis on which to begin to construct a physical geometry from the standpoint of Brunelleschi, Leibniz, Gauss, Riemann and LaRouche.

To grasp this, think of the difference between abstract geometrical shapes, and the physical geometry of bricks and mortar.

Start with a vertical column. An abstract geometrical line, according to Euclid, is that extension in empty space which has only length. No matter how long the line, its width, is always the same, namely, nil. However, when building a vertical column (line) of bricks, the higher the column, the greater the pressure on the lower bricks. To build the column higher requires strengthening the lower portions of the column, by increasing its width, or by some other means.

Extend this thought to an area. From the standpoint of empty Euclidean space, an area is that which has length and width. A bounded area is enclosed by a line either straight or curved. A physical area, however, is enclosed by a physical structure, the shape of which is determined by physical principles. One approach to enclosing a physical area, would be to build two vertical columns and span those columns with a flat roof. But, this is a relatively weak structure, as the roof is only strong near where it is supported by the columns. The farther apart the columns are, the weaker is the roof. (See Figure 3.)

Figure 3

A far more stable structure for vaulting a vertical area is an arch. The circle is at first thought the simplest type of arch, because the circular boundary encloses the largest area by the least perimeter. If the arch is designed so that all the bricks point to the center of the circle, the arch will be relatively stable upon completion. (See Figure 4.) But, while under construction, the arch cannot support itself, requiring the use of a temporary scaffolding to support the arch under construction. Thus, the arch is self-supporting as a whole, but not in its parts.

Figure 4

The circular arch poses another problem. Even though it encloses the greatest area with the least perimeter, its height is a function of its width and the line of pressure does not conform to the circular curve. (See Figure 5.)

Figure 5

To enclose a taller area requires a wider arch which in turn decreases the overall stability of the structure because the downward pressure from the upper bricks pushes the sides of the arch outward. Thus, even though, from the standpoint of abstract geometry, the circle is isoperimetric, from the standpoint of physical geometry, some other shape provides the greatest stability for the tallest area. The shape that achieves this is a pointed arch in which the two arcs that make up the arch are circular arcs with different centers. (See Figure 6.) The pointed arch, thus, not only encloses a taller area, but is more stable because the curvature of the arch conforms more closely to the physical line of stresses in the structure. In other words, the shape of the arch is determined not by abstract geometrical characteristics but by physical ones.

Figure 6

Now, to the problem facing Brunelleschi enclosing a volume. Geometrically, a volume is enclosed by a surface, which is produced when a curve is moved. For example, from the famous construction of Archytas, when a circle is moved along a line, a cylinder is produced; when rotated around a point, a torus is produced; and when rotated around a line, a sphere is produced. And so, a dome can be produced by rotating an arch, either circular or pointed around an axis. (See Figure 7.)

Figure 7

But, a physical surface, such as a dome, is not simply a rotated arch, because a new set of stresses occurs in the dome that does not occur in the arch. In addition to the stresses along the arch, (from top to bottom, i.e., longitudinal), there are stresses around the dome (circumferential or hoop).

So, the problem Brunelleschi faced in building the Dome of the required size was to design a structure whose shape would balance these stresses without requiring external buttressing which would diminish the Dome’s beauty and undermine its effectiveness for changing society by changing the minds of the population.

Additionally, a dome, like an arch, generally requires a supporting scaffold, or centering, to hold it up until its completion. Here, Brunelleschi faced his most formidable obstacle. The Dome over Santa Maria del Fiore was so big that there was not enough wood available to build such a large scaffolding. Consequently, Brunelleschi took the bold step of building the Dome without centering, requiring him to construct a dome that was self-supporting in its whole and its parts. Such a shape could not be determined by the methods associated with Euclidean geometry. The shape Brunelleschi required was determined only by physical principles.

To do this, Brunelleschi decided to construct two domes, one inside the other, with a stairway between them. Both would conform to the pointed arch form called for in the original design. However, according to the architect Bartoli, (see 1989 21st Century) the curve of the inner dome was a based on a circle whose diameter was three fourths the inside diameter of the octagonal drum (pointed fourth) while the outer dome’s curvature was four-fifths the outer diameter (a pointed fifth) (See Figure 8.)

Figure 8

Since the use of centering had to be avoided, Brunelleschi had to control the curvature of both domes very carefully as the were being constructed. This entailed controlling three different curvatures: the longitudinal curvature; the circumferential curvature; and the curvature inward towards the center of the Dome. If all three curvatures could be controlled during all phases of construction, the Dome would not only be stable upon completion, but each stage would be stable enough to be a platform from which the next stage would be built. Thus, the Dome had to conform to a shape that would be self-supporting in its whole and its parts.

Brunelleschi had to solve a multitude of problems, each requiring revolutionary new ideas to accomplish the task. But, the discovery most central to his success, the one most relevant for the future development of the anti-Euclidean physical geometry of Kepler, Fermat, Leibniz, Gauss and Riemann, is the one identified by LaRouche. Brunelleschi used a hanging chain to guide the development of the curvature of the dome at each stage of construction. Thus, the overall shape of the Dome was determined, not by a curvature defined by abstract mathematics, but by a physically defined principle. Just as a hanging chain is self-supporting in its whole and its parts, the Dome, whose curvature is guided by the curvature of the hanging chain, is, likewise, self-supporting surface, in its whole and its parts.

The beauty of the Dome demonstrates the truth of Brunelleschi’s discovery, but, it would take the discoveries of Kepler, Fermat, Leibniz, Gauss, Riemann and LaRouche to fully grasp the underlying principle.

The Development of the Physical Idea of Shape

The success of Brunelleschi’s Dome demonstrated that the architectural principles of physical geometry on which it was based were universal. This view was expressed by Johannes Kepler, who approximately 150 years later wrote concerning the construction of the solar system in his Mysterium Cosmographicum, “We perceive how God, like one of our own architects, approached the task of constructing the universe with order and pattern, and laid out the individual parts accordingly, as if it were not art which imitated Nature, but God himself had looked to the mode of building of Man who was to be.”

Kepler went on to develop, in that work and in his subsequent New Astronomy and Harmonies of the World, that the shape of the solar system, like the Dome, was determined not by considerations of abstract mathematics, (which would have indicated perfectly circular orbits) but by physically determined harmonic principles. Thus, the elliptical planetary orbits, like Brunelleschi’s Dome, were the size and shape that they had to be in order to express the harmonic relationships of those physical principles.

This physically determined idea of shape took another step in its development with Fermat’s determination that the shape of the pathway of light was determined by the principle of shortest-time:

“Our demonstration is based on the single postulate, that Nature operates by the most easy and convenient methods and pathways — as it is in this way that we think the postulate should be stated, and not, as usually is done, by saying that Nature always operates by the shortest lines … We do not look for the shortest spaces or lines, but rather those that can be traversed in the easiest way, most conveniently and in the shortest time.”

Leibniz, following up on the discoveries of Kepler and Fermat, generalized these discoveries as a universal principle of least-action:

“…the Architect of all things created light in such a way that this most beautiful result is born from its very nature. That is the reason why those who, like Descartes, reject the existence of Final Causes in Physics, commit a very big mistake, to say the least; because aside from revealing the wonders of divine wisdom, such final causes make us discover a very beautiful principle, along with the properties of such things whose intimate nature is not yet that clearly perceived by us, that we can have the power to explain them, and make use of their efficient causes, along with their artifacts, such as the Creator employed them in order to produce their results, and to determine their ends. It must be further understood from this that the meditations of the ancients on such matters are not to be taken lightly, as certain people think nowadays.”

Leibniz’ most far reaching discovery of this principle of least-action, made in collaboration with Johann Bernoulli, demonstrated that the catenary, the guiding principle of Brunelleschi’s Dome, embodied the most universal expression of least-action. As we’ve developed in other locations, the physical characteristic by which the hanging chain supports itself, expresses all the elementary transcendental relationships of geometry: the circular, hyperbolic, and the powers associated with lines, surfaces and volumes. (See Figure 9.)

Figure 9

Look back at our earlier comparison of the difference between abstract geometrical notions of line, area and volume, with the physical requirements of constructing a column, arch and dome. As is already implicit in the concept of powers developed by Pythagoras, Archytas, Plato, et al., even the purely geometrical concepts of line, area and volume are ultimately determined by the physical principles which Leibniz demonstrated are expressed by the catenary. The idea of lines, areas and volumes, separated from this idea of power as universal physical principles, is as chimerical as the mystical powers of the Roman Pantheon.

From Pathways to Surfaces

Brunelleschi’s Dome points the way to a still further development of the universal principle of least-action. Planetary orbits, the curvature of light, and catenaries are all pathways, i.e. curves. Brunelleschi’s Dome is a least-action surface.

The concepts to understand this distinction were developed by Gauss who, looking back as we’ve been doing, on the discoveries of Kepler, Fermat and Leibniz, developed the foundations of a physical theory of surfaces.

The context for Gauss’ discovery was his measurement of the surface of the Earth, which, because it is physically determined, must, in keeping with Leibniz’ principle, be a least-action surface. Over a more than 20 year period, Gauss made careful astronomical and geodetical measurements of the Earth. Abstract geometrical considerations would suggest that the Earth would be a perfect sphere, because the sphere enclosed the largest volume inside the smallest surface. But, because the Earth is a rotating body in the solar system, its physical shape is not spherical, but ellipsoidal.

As we have developed in earlier pedagogicals, Gauss’ measurements led him to discover that the physical shape of the Earth was not ellipsoidal, but something more irregular. He identified the, “geometrical shape of the Earth, as that shape which is everywhere perpendicular to the pull of gravity.” In other words, Gauss did not try to fit the Earth into a shape pulled from the text books of abstract mathematics, rather, he invented a new geometry that conformed to the physical characteristics of the rotating Earth.

Gauss reported the generalization of his discoveries in his 1822 Copenhagen Prize Essay, on conformal representation and his 1827, “General Investigations of Curved Surfaces”. Future pedagogicals will develop these concepts in greater detail, while here we focus on the general ideas most relevant to this discussion.

For Gauss, all surfaces had a characteristic curvature, which in turn determined certain least-action pathways, that he later called, “geodesics”. For example, in a plane, the geodesic is a straight-line, while on a sphere, the geodesic is a great circle. In these two cases the curvature is uniform and so the geodesic is the same every where on the surface. In contrast, an ellipsoid, for example, is a surface of non-uniform curvature. Consequently, the geodesic is different depending on its direction and position on the surface. (See Figure 10.)

Figure 10

To illustrate this, the reader is encouraged to do some physical experiments. Take a plane, sphere, spaghetti squash or other irregular shaped object. Mark two points at different places on the surface and stretch a thread between them so that the thread is taught. The thread will conform approximately to the geodesic between those two points. Notice that on the plane, the geodesic is always a straight line, while on the sphere it is always a great circle, while on the squash, the geodesic changes from place to place, and direction to direction.

There is a further distinction between the plane and the sphere or ellipsoid. On the plane there are an infinite number of pathways between any two points, but only one of these paths is a geodesic, i.e. least-action. This is also true on a sphere or ellipsoid, except, if the two points are at the poles. Then there are an infinite number of geodesics between these two points. Thus, the bounded nature of the sphere and ellipsoid, produce a singularity with respect to the nature of the geodesics. The significance of this distinction will become more clear as we develop more of Riemann’s geometry in future pedagogicals.

What Gauss investigated was the general principles by which the curvature of the surface determined the characteristic of the geodesic. Of immediate relevance for this discussion is Gauss’ determination of a means to measure the curvature of the surface at any point. It is sufficient for our purposes here to illustrate this by a physical demonstration. On the squash, draw a circle by tying a marker to one end of the thread and rotating it while holding the other end of the thread in a fixed position. The radii of this circle are all geodesics in different directions. Now examine the curvature of each geodesic, which will vary for each direction. However, one geodesic will be the least curved, while another will be the most curved. Now, try this on a different type of surface, such as a butternut squash shaped like a dumbbell. The part of the round ends of the butternut squash have the same characteristic as the spaghetti squash, in that the center of curvature is always inside the squash. But, in the middle of the squash something different happens. Here the center of curvature is either inside or outside the squash, depending on the direction of the geodesic. This characteristic Gauss called, “negative curvature” and is the characteristic of curvature expressed by a surface formed by a rotated catenary called a catenoid. (See Figure 11.)

Figure 11

Brunelleschi’s Dome expresses this characteristic of negative curvature.

Furthermore, Gauss proved that on any surface, no matter how irregularly it was curved, the geodesics of maximum and minimum curvature would always be at right angles to each other!

Thus, at any place on a surface, the curvature of the surface expresses a physical principle that in turn determines the geodesic, or least-action pathway within that surface.

From Surfaces to Manifolds

Working from Gauss’ discovery, Riemann generalized this concept still further to the idea of a geodesic within a manifold of universal physical principles. The manifolds cannot be directly visualized but the characteristics of that manifold can be directly determined by a change in geodesic.

For example, light under reflection and refraction follows a pathway within a surface, but each type of action expresses a different pathway because the physical manifold of refraction includes a principle, changing speed of light, that does not exist within the manifold of reflection. The addition of this new principle to the manifold of action, changes the geodesic.

Riemann developed the means to represent these higher manifolds by complex functions. For example, as was developed in the previous pedagogical, the conic section orbits and catenary are both least-action pathways with respect to the manifold of universal gravitation. In other words, each represents a changing geodesic with the manifold of universal gravitation. But, when the catenary is expressed as a function in the Gauss/Riemann complex domain, the conic section orbits are seen as a subsumed geodesic within the higher principle represented by the catenary. (See Riemann for Anti-Dummies Part 40.)

More general examples are illustrated in the accompanying animations. These illustrate how the same action, when carried out in different manifolds, is changed by the characteristics of the manifold. Think of the orthogonal nets in each figure as the minimum and maximum geodesics in each manifold. The loopy curve maintains the same angular orientation with respect to these geodesics in each case. But, because the geodesics change, from manifold to manifold, the action changes. Thus, a change in the principles that determine the manifold, change the geodesics, which in turn change all action within that manifold. Conversely, to effect a physical change in any action, one must act to change the characteristics of the manifold.

z2

z3

ez

1/z

Catenary

Now look at Brunelleschi’s Dome from this standpoint. The Dome is a surface whose geodesic, in principle, conforms to the catenary. As a least-action surface, it expresses a geodesic with respect to the principle of universal gravitation. With respect to the manifold of universal history, building the Dome was the geodesic from that dying culture of the Roman Empire to the Renaissance.

At our present place in the manifold of universal history, building LaRouche’s youth movement combat university on wheels and making LaRouche President of the United States, is for us, Brunelleschi’s Dome– the geodesic from this dark age to our Renaissance.

Riemann for Anti-Dummies Part 40

COGNITIVE LEAST ACTION

Throughout his various works on complex functions, Riemann notes that the hidden harmonies of the complex domain, not calculations, are the least action pathways for the discovery of truth.

Riemann’s concept is in keeping with the tradition from Plato to Gauss, as exemplified by Gauss’ determination of the orbit of Ceres. In that case, every leading astronomer attempted to deduce Ceres’ orbit by an ever increasing level of calculations upon the few data points of observations supplied by Piazzi. All failed. Gauss, on the other hand, focused on Kepler’s harmonic principles, finding Ceres’ orbit as a consequence of them. Where the failures calculated unknown data from known data, Gauss sought the principles that determined both the known and unknown data. Gauss later distinguished his method from the failed ones with reference to Euler’s famous attempt to deduce the orbit of a comet by detailed calculation, an effort that left Euler blind in one eye. “I too would have gone blind,” Gauss is reported to have said, “If I calculated like Euler did.”

As urgent and necessary as it is for political leaders to grasp Gauss’ and Riemann’s method, it nonetheless presents serious psychological difficulties for those reared in the fantasy world of the post-1966 consumer society. As noted in last week’s installment, consumers only know objects and how to manipulate them. Acting on the world is limited to manipulating those objects according to a set of authoritative rules. Consumers look in awe to those other consumers who appear to manipulate the greatest number of objects. (Modern academics call this objective science.) It is no wonder that under conditions of systemic collapse, such consumers become fear-driven pessimists.

Yet, to act on the world as Gauss and Riemann did, requires a capacity of mind to grasp not things, but relationships. Not merely relations among things, but relationships among sets of relations. This, as Gauss and Riemann demonstrated, is the province of the complex domain.

To further illustrate this point, look at the principle of universal gravitation. As a principle, universal gravitation is not expressible by a number, such as 32/feet/second/second. Nor is it expressible by an algebraic formula such as the inverse square law. Principles, to be truly comprehended, can only be known by how they act on other principles. As such, principles must be thought of only by Riemann’s concept of a manifold. Under Riemann’s idea of a complex function, the mind acts, not on things, but on manifolds of principles.

This concept is well developed by Kepler’s succession of discoveries with regard to planetary motion, from the astronomical significance of the Platonic solids, to the elliptical orbits, to the harmonic proportions among the orbits. Each of the above principles expresses a set of relations. Universal gravitation expresses the relationship among these sets of relations.

The Leibniz/Bernoulli principle of the catenary similarly expresses a set of relations, ordered by the principle of universal gravitation. As will be illustrated below, the complex domain affords us the power to comprehend the unifying relationship of universal gravitation between these two sets of seemingly different relations.

Before exploring more specifically the manifold of universal gravitation, it were beneficial to engage in a short warm-up exercise. Look again at a simple example of a complex function, for example, the complex function that corresponds to the general principle of doubling the square. (See figure 1a, figure 1b, and figure 1c.)

Figure 1a

Figure 1b

Figure 1c

Use this example to begin to wrench your mind away from the consumerist fixation on things, so as to be able to better grasp the physical example that will follow. In this example, think of the orthogonal grid of lines depicted on the left side of 1b not as a collection of lines and points, but as a metaphorical representation of a set of ideas related to each other in that way. Each idea is represented by a complex number, which denotes a unique action. (That action is always with respect to some origin, which is always defined by some physical singularity.) The lines connecting the points can be thought of, metaphorically, as least action pathways, i.e. geodesics, with respect to the principle of organization of the manifold of ideas represented.

Now, a new principle is introduced, in this example the principle of doubling the square. The introduction of that principle transforms all the straight-line relationships into parabolic pathways. The introduction of such a new principle, transforms all the relationships of the manifold, all at once, without, so to speak, calculation. To properly grasp this conception, resist the tendency to think of the grid of lines as a thing and the grid of parabolic pathways as another thing. Rather, think of one manifold– a polyphony evoked by the introduction of the new principle of squaring, which changes the “geodesic” within each set of relations. (See animation 1.)

Animation 1

Armed with this warm up, move on, to a physical example:

What is the connection, with respect to the principle of universal gravitation, between the least action pathway expressed by the catenary and the least action pathways expressed by the conic section planetary orbits of Kepler and Gauss? This can only be grasped from the standpoint of the complex domain.

Begin with Leibniz’ discovery that the catenary expresses the arithmetic mean between two exponential (logarithmic) functions. (See figure 2.)

This is already a precursor of Riemann’s idea of a complex function. Think of each exponential not as a “graph” as you were taught in school, but, as, Leibniz did, as a relationship of two relationships, the arithmetic and the geometric. (See figure 3.) Thus, the catenary expresses a relationship between two sets of arithmetic-geometric (exponential/logarithmic) relations.

Figure 3

But, as Riemann noted, when this relationship among sets of relations is viewed from the standpoint of the complex domain, “a regularity and harmony emerge that otherwise remain hidden.”

Look, first, at the exponential/logarithmic relationship in the complex domain. To do this, we must think, as Gauss did, of the complex domain as represented by a doubly-extended surface, with a physically determined origin, in this case, the lowest point of the catenary. Each point on the surface represents a complex number which itself denotes a unique exponential action. (See figure 4.)

Figure 4

Complex numbers represented by points equally spaced along a line are related to each other arithmetically. Complex numbers represented by points along a spiral, are related to each other geometrically. Thought of in this way, a grid of lines expresses an arithmetic relationship between complex exponentials. (See figure 5.)

Figure 5

The points along any one line are arithmetically related complex numbers. Lines that are equally spaced to other lines, (such as those in the grid) are arithmetically related sets of arithmetically related complex numbers.

Now, take this relationship so described, and use that as a principle of transformation of the complex domain itself. (See animation 2.)

Animation 2

This transformation expresses, from the higher standpoint of the complex domain., the relationship between the arithmetic and geometric that was otherwise previously expressed by Leibniz, et al. with respect to exponential, circular and hyperbolic functions. The complex exponential transforms the arithmetic relationships into geometric ones, creating a sort of arithmetic-geometric relationship among arithmetic-geometric relationships. Here, the arithmetically related (equal spaced), vertical lines become circles whose radii are geometrically related. The points along each line that are arithmetically related (equally spaced) become equally spaced points along the arcs of the circles. Inversely, the arithmetically related (equally spaced) horizontal lines become equally spaced radii, while the arithmetically related (equally spaced) points along each horizontal line, become geometrically related points along each radii. (See figure 6.)

Figure 6

When one considers the circles as special cases of spirals, the equally spaced radii and equally spaced points along the arcs are also in geometric relationship to each other as well.

Now take the next step, and apply Leibniz’ principle of the catenary as the arithmetic mean between two exponentials in this complex domain. The arithmetic mean between two inversely related circles forms an ellipse. (See animation 3.)

Animation 3

The arithmetic mean between two inversely related radii forms an hyperbola. ( See animation 4.)

Animation 4

The totality of this transformation forms an orthogonal array of ellipses and hyperbolas which correspond to the least-action pathways of the catenary in the complex domain. (See figure 7, and animation 5.)

Figure 7

Animation 5

Thus, Leibniz’ catenary principle, expressed in the complex domain of Gauss and Riemann expresses a manifold of elliptical and hyperbolic least-action pathways. In other words, the complex domain, as that domain in which we can represent as shadows, the manifold of relationships among sets relationships, increases the cognitive power of the mind, such that we become able to comprehend universal gravitation, as a principle of unity of least action among the catenary and conic section planetary orbits, and, of course, much, much, more.

Riemann For Anti-Dummies Part 39

To paraphrase Nicholas of Cusa, consumers, like animals, don’t count. They have no concept of number. Their mental world is made up only of the things they consume. How those things are produced, what power generates such things, is beyond their ken. Numbers, for them, are mere symbols, that, when manipulated according to a learned set of authoritative rules, (such as the rules of money), have some unexplainable, but psychologically powerful, connection to the things they consume.Such numbers don’t count.

“Number”, according to Cusa, is, “unfolded reason … theprime exemplar of the mind”. In the Pythagorean tradition of Plato, Cusa recognized that numbers don’t count things. Number is the means by which the mind comprehends relations. Not simple relationships among things, but the relationships among relationships. “We conjecture metaphorically from the rational numbers of our mind in respect to the real ineffable numbers of the divine Mind, we indeed say that number is the prime exemplar of things in the mind of the Composer, just as the number arising from our rationality is the exemplar of the imaginal world.”

This capacity is a unique human characteristic and is bound up with man’s capacity to increase his power in and over the universe. As Prometheus states in Aeschylus’ drama, Man was, “in an ignorant condition, living in holes and– … utterly without knowledge, until I taught them to discern the rising of the stars and their settings, which are difficult to distinguish. Yes, and numbers, too, chiefest of sciences, I invented for them, and the combining of letters, creative mother of the Muses’ arts, with which to hold all things in memory….”

This is the concept of number specific to a healthy producer society. For the consumer milk comes from the supermarket. There is no concept of number associated with this idea other than the symbol appearing on the display of the cash register in response to a computer scanning of a bar code. Contrast this to the numbers that express the relationship of that milk in the supermarket to the dairy farm and transportation system that produced the milk and transported it to the store. Now, think of the higher concept of number associated with the multiply-connected manifold of abiotic, biotic, and cognitive processes that comprise the physical economic relationships of the above transaction. Think still higher of the numbers associated with the multi-generational trajectory in which that multiply-connected physical economic manifold resides. And, still higher to the numbers associated with the manifold of universal principles — those discovered and those still yet to be discovered — which have the power to change that trajectory and all that follows from it.

The productive power of the mind counts, and it counts with complex numbers.

To grasp the concept of complex numbers requires the mind be wrenched away from those neurotic, consumerist tendencies that associate numbers with sensible objects. For that reason, a careful study of Gauss’ “Disquisitiones Arithmeticae” is highly recommended, as anyone who has had the pleasure of unfolding its wisdom will attest. By the time Gauss composed this opus, at the age of 22, he had already a fully-developed concept of the complex domain, as indicated in the climactic seventh section on the division of the circle. That section, although last in the book, was written first, and the principles expressed there unfold from the opening motivic idea of the work Gauss’ concept of congruence.

Gauss generalizes Kepler’s notion of harmony by establishing numbers with respect to their intervallic relationship, as distinct from the sense-certainty concept of things. Illustrate this idea (as we have in past pedagogicals) with a simple example. Draw five dots in roughly a circle. Label these dots 0, 1, 2, 3, 4, respectively. Now, connect these dots in sequence. Call that sequence 1. Next, connect every other dot. Call that sequence 2. Next, connect every third dot. Call that sequence 3. The same with every fourth dot. Connecting every fifth dot leads nowhere. Now, try every sixth, seventh, etc.

Calling five a modulus, Gauss’ concept of congruence establishes each number by its relationship to all other numbers with respect to modulus five. You should have noticed that sequence 1 and 6, 2 and 7, 3 and 8, etc. produced the same results. Such relationships were called by Gauss “congruent with respect to modulus five”. (The difference between two congruent numbers is equal to the modulus.) Also, sequence 2 produced the same result as sequence 3, except in opposite direction. A similar relationship was produced for 1 and 4. Introducing “-“to denote direction, Gauss’ congruence is also expressed by the relationships of 1 to -4; 4 to -1; 2 to -3; and 3 to -2.

Think back over this simple exercise. The numbers0, 1, 2, 3, 4, -1, -2, -3, -4, always denote relationships, not things. The initial numbers, 0, 1, 2, 3, 4, denote the relationship of each individual dot to all five. The sequence numbers, both positive and negative, denote relationships among these relationships.

Thus, the modulus, in this case five, denotes not five things, but a type of intervallic relationship among relationships. Inversely, the domain of such relationships denotes five as a prime number, as it establishes a total number of relationships equal to 5 minus 1. (It is suggested the reader try the above experiment with moduli 6, 7, 8, 9, 10, 11 to establish this concept more fully in your mind.)

Underlying these relationships is the “dimensionality” of the domain in which they arise. Each number and each sequence followed its predecessor by the same difference by which it was followed by its successor, i.e., arithmetically. Now, extend this investigation into a doubly-connected, i.e., geometric, domain. To do this think of 1,2,3,4 as sides of squares. 1 and4 produce squares of area 1 and 16 respectively, which, with respect to modulus five are both congruent to 1. 2 and 3 produce squares of 4 and 9 respectively, which with respect to modulus 5are congruent to -1. Thus, with respect to modulus 5, both 1 and-1 are squares! 1 and 4 are ?1, and 2 and 3 are ?-1 modulo 5! For this and related reasons, Gauss insisted that ?-1 be given “full civil rights” with all other numbers, and the domain of numbers should be extended to include them.

“The mathematician always abstracts from the constitution of objects and the content of their relations. He is only concerned with counting and comparing these relations; in this sense he is entitled to extend the characteristic of similarity which he ascribes to the relations denoted by +1 and -1 to all four elements +1, -1, i (?-1) and -i (-?-1),” Gauss wrote in the announcement to his second treatise on biquadratic residues.

Gauss insisted, and repeatedly stated, that this, “complex domain” was a higher concept that existed outside the domain of the senses, but, “the true metaphysics of these magnitudes could be placed in a most excellent light”, by representing these relationships as a quadratic array on a doubly extended surface:

“To form a concrete picture of these relationships it is necessary to construct a spatial representation, and the simplest case is, where no reason exists for ordering the symbols for the objects in any other way that in a quadratic array, to divide an unbounded plane into squares by two systems of parallel lines, and chose as symbols the intersection points of the lines. Every such point A has four neighbors, and if the relation of A to one of the neighboring points is denoted by +1, then the point corresponding to -1 is automatically determined, while we are free to choose either one of the remaining two neighboring points, to the left or to the right, as defining the relation to be denoted by + i. This distinction between right and left is, once one has arbitrarily chosen forwards and backwards in the plane, and upward and downward in relation to the two sides of the plane, in and of itself completely determined, even though we are able to communicate our concept of this distinction to other persons only by referring to actually existing material objects.*

[* Kant already had made both of these remarks, but we cannot understand how this sharp-witted philosopher could have seen in the first remark a proof of his opinion, that space is only a form of our external perception, when in fact the second remark proves the opposite, namely that space must have a real meaning outside of our mode of perception.]

“The difficulty, one has believed, that surrounds the theory of imaginary magnitudes, is based in large part to that not so appropriate designation (it has even had the discordant name impossible magnitude imposed on it). Had one started from the idea to present a manifold of two dimensions (which presents the conception of space with greater clarity), the positive magnitudes would have been called direct, the negative inverse, and the imaginary lateral, so there would be simplicity instead of confusion, clarity instead of darkness,” Gauss wrote in his second treatise on biquadratic residues.

Thought of in this way, each complex number denotes a two-fold complex of direct and lateral action, or, rotation and extension. The physical example Gauss gave for this relationship was the motion of the bubble in a plane leveller. The bubble could only move back and forth if the ends of the level moved up and down.

Gauss’ idea of complex numbers extends his concept of congruence, by which the relationships among numbers are grasped, to the complex domain, by which relationships among a set of relations can be comprehended. Just as his earlier concept of a modulus expressed a simple intervallic relationship among numbers, the complex modulus expressed a complex interval. (See figure 1a, and figure 1b.)

Riemann for Anti-Dummies Part 38

YOU ARE NOT IMPOSSIBLE

When Gauss set about writing his 1799 dissertation on what he called, “The Fundamental Theorem of Algebra,” he had already in his mind a fully developed concept of the complex domain as the idea that penetrated most deeply into the metaphysics of space, and he would spend the rest of his life unfolding the implications of that youthful discovery. But, in order to achieve what he would later call, “full civil rights for complex numbers,” he first had to root out the source of their oppression: the popular acceptance of Euler’s diktat that such numbers were “impossible.”

What one considers “impossible” is, fundamentally, a function of one’s concept of what is “possible.” Think of the foolishness today of those who insist that what Lyndon LaRouche says must be done, (most emphatically his electability as President of the United States) is “impossible.” Their tragic mistake flows not from any reasoned, scientific assessment of the matter. They assert its impossibility because they don’t want to face the possibility that their continued existence is possible only if what they think is “impossible” actually happens.

In one of his epistemological fragments, Bernhard Riemann spoke of the significance of the possible for science:

“Natural science is the attempt to understand nature by means of exact concepts.

“According to the concepts through which we comprehend nature our perceptions are supplemented and filled in, not simply at each moment, but also future perceptions are seen as necessary. Or, to the degree that the conceptual system is not fully sufficient, future perceptions are determined beforehand as probable; according to the concepts, what is “possible” is determined (thus what is `necessary’ and conversely, impossible). And the degree of possibility (of `probability’) of each individual event which is seen as possible, in light of these concepts, can be mathematically determined, if the concepts are precise enough.

“To the extent that what is necessary or probable, according to these concepts, takes place, then this confirms the concepts, and the trust that we place in these concepts rests on this confirmation through experience. But, if something takes place that is unexpected according to our existing assumptions, i.e. that is impossible or improbable according to them, then the task arises of completing them or, if necessary reworking the axioms, so that what is perceived ceases to be impossible or, improbable. The completion or improvement of the conceptual system forms the `explanation’ of the unexpected perception. Our comprehension of nature gradually becomes more and more complete and correct through this process, simultaneously penetrating more and more behind the surface of appearances.

“The history of causal natural science, in so far as we can trace it back, shows that this is, in fact, the way our knowledge of nature advances. The conceptual systems that are now the basis for the natural sciences, arose through a gradual transformation of older conceptual systems, and the reasons that drove us to new modes of explanation can always be traced back to contradictions and improbabilities that emerged from the older modes of explanation.”

By maintaining the “impossibility” of complex numbers, Euler, (whose patrons were the enemies of the American Revolution), along with J.L. Lagrange, (Napoleon’s favorite mathematician), sought not merely to exclude such magnitudes from mathematical calculations. Both Euler and Lagrange made liberal use of these “impossible” magnitudes in formal calculations. Rather, Euler et al. sought to exclude the possibility that the human mind could penetrate beneath the surface of appearances into the deeper domain of, what Plato called “powers,” where complex numbers arise.

In his 1799 dissertation Gauss attacked Euler’s method directly:

“If imaginary quantities are to be retained in analysis at all (which seems for several reasons more advisable than to abolish them, once they are established in a solid manner), then they must necessarily be considered equally possible as real quantities; for which reason I would like to comprise the reals and the imaginaries under the common denomination of {possible quantities}: Against which I would call {impossible} a quantity that would have to fulfill conditions that could not even be fulfilled by allowing imaginaries.”

The existence of complex numbers was not only possible: It was necessary to comprehend what ultimately made all numbers possible.

To establish this, Gauss tapped into the deep vein of investigations that goes all the way back to the Pythagoreans, who understood number as the means by which the mind expresses the harmonic principles that lie beneath the shadow of sense perception.

Writing in “On Learned Ignorance,” Nicholas of Cusa described this concept of number this way:

“All those who investigate, judge the uncertain by comparing it to a supposed by a system of proportions…. But the proportion which expresses agreement in one aspect and difference in another, cannot be understood without number. That is why number embraces everything which is susceptible of proportions. Thus, it not only creates proportion in quantity, but in every respect through which, by substance or accident, (two things) might agree and disagree. Thus, Pythagoras rigorously concluded that everything is constituted and comprehended through the power of numbers.”

Number has the power to express powers through proportions. Complex numbers express proportions among powers.

For example, the power to double a square is expressed through the geometric proportion 1, 2, 4, 8, 16, 32, etc., even though the magnitude that doubles the square is incommensurable to all these numbers. Furthermore, the power that doubles the cube is also expressed, but in a different way, by the same proportion, (as two geometric means between two extremes instead of one), even though the magnitude that doubles the cube is also incommensurable to all those numbers.

From this standpoint, all numbers can be generated by a succession of powers, and this is what is meant by the term, “logarithm”–a term coined by John Napier in 1594 from the Greek words “logos” and “arithmos.”

The most general form of this concept is expressed by Jakob Bernoulli’s equiangular spiral and Huygens’ hyperbola. In the former, all possible magnitudes are expressed by the radii whose lengths are a function of an angle of rotation. Proportional lengths correspond to equal angles (see Figure 1).

Figure 1

In the latter, all possible magnitudes are expressed by lengths along the asymptote that correspond to equal areas (see Figure2).

Figure 2

In both cases all possible positive quantities are expressed, inversely, as a function of a power, expressed as either an angle (spiral) or an area (hyperbola).

In both cases, adding the logarithm (angle or area) produces proportional changes in length.

As discussed in the previous installment of this series, Leibniz brought a crucial contradiction to light by posing the question, “What has the power to produce a negative number?” This provoked a dispute with his collaborator Johann Bernoulli, who insisted that negative numbers were produced by the same powers as positive numbers. Leibniz, on the other hand, correctly disagreed. For Leibniz the very existence of negative numbers (which had been called “false” numbers) demanded a higher principle, which Gauss later discovered as the complex domain.

For Gauss, negative numbers were not absolute quantities. They were physically determined. In numerous locations, Gauss repeatedly polemicized, (against I. Kant) that the difference between positive and negative, right and left, up and down, could not be determined by mathematics but only with reference to physical action.

Look at this from the standpoint of the above illustrations of the spiral and hyperbola. Both generate all possible magnitudes as a function of powers. But, in both cases, the exact same result can be obtained, but in exactly the opposite orientation (see Figure 3 and Figure 4). In Figure 3, you can see two spirals that produce the same magnitudes, but in different directions.

Figure 3

In Figure 4 you can see two branches of an hyperbola that produce the same magnitudes, but in different directions.

Figure 4

In each case, if one set of magnitudes is denoted positive numbers the other set can be denoted negative. But, as Gauss pointed out, there is no {a priori} way to distinguish one from the other. Only when presented with both, is the existence of positive and negative established.

But, there is a still deeper, much more profound principle embedded in this. Look at the transition between the positive and negative hyperbola. The vertical asymptote is an “infinite” boundary separating positive from negative. Similarly, for the spirals. The transition from the positive to the negative spiral is the point of the change in direction, which each spiral approaches, but never crosses.

Thus, the domain in which both positive and negative numbers exist together must be of a higher power, where the powers that generate powers reside. It comprises Gauss’ domain of all possible (complex) quantities.

Like all ideas, Gauss recognized that this domain could not be seen directly, but, it, nevertheless, was susceptible of metaphorical representation. Since it was the domain of powers, it could not be represented by simple proportions among things, but as a proportion between proportions. Consequently, each complex number represented a proportion, not a quantity. The manifold of complex numbers, Gauss said, could only be represented on a surface extended in two directions. The physical example Gauss used was the geodesist’s plane leveller. The position of the bubble at rest is determined by both the axis of the tube and the direction of the pull of gravity, which is perpendicular to it.

On Gauss’ surface each point represented a power that was denoted by a complex number. Using some physically determined point and line as a reference, each power, i.e., each complex number is generated by a spiral action rotation and extension (see Figure 5).

Figure 5

In this way, proportions between proportions could be represented.

For example, a power acting on a power. In Figure 6 and Animation 1, complex number a+bi represents a power produced by a combination of rotation and extension. When that power acts on itself, it produces (a+bi)². When it acts on itself again it produces (a+bi)³, etc. What results is a series of similar triangles conforming to an equiangular spiral. While this spiral looks similar to Bernoulli’s spiral, it is different. Bernoulli’s spiral represents a succession of powers that produce simple magnitudes. Gauss’ complex spiral represents a higher power that produces a succession of powers, not simple magnitudes.

Figure 6

Animation 1

Figure 7, illustrates the more general case of the proportion between two different powers, or, what is commonly known as multiplication. Here the complex number 2 + i is multiplied by 1 + 2i to form 5i. In this case the 2 + i forms the red triangle with vertices 0, 1, 2 + i. The product is the point (5i) which forms the similar triangle with 0, 1 + 2i as its base. (The schoolbook arithmetic idea of multiplication as a set of rules is brainwashing. As Gauss emphasized, multiplication is a proportion such that 1: a :: b: a x b. You, the reader, are left to confirm this for yourself experimentally. Try experimenting with Theatetus’ squares and rectangles.)

Figure 7

As in the previous examples of the hyperbola and spiral, the proportional changes in extension are “connected” by adding the angles (logarithm) and multiplying the lengths.

RIEMANN FOR ANTI-DUMMIES PART 37

THE DOMAIN OF POSSIBILITY

Plato, speaking in the Laws through the voice of an Athenian stranger, holds it indispensable for leaders of society to possess elaborate knowledge of arithmetic, astronomy and the mensuration of lines, surfaces and solids. He also considers it a disgrace for any common man to lack a basic understanding of these same subjects.

It is altogether fitting that these words should issue from someone far from home, for, as Helga Zepp-LaRouche so artfully demonstrated in her presentation to the ICLC Labor Day Conference, by the time of Plato’s writing ,Athenian culture had estranged itself from these concerns and embarked on that chain of events which led to the disastrous Peloponnesian Wars. It is further fitting that Plato speaks here as a stranger, as all three subjects share a common focus on the exploration of those universal principles that govern, but don’t reside, in the domain of objects and sense perception. To one trapped in the domain of the senses, those principles appear to come from some foreign land “over the horizon”, or, “beyond the finite” . But, to one willing to ascend to its not too distant shores, that place is the province from which come the common principles, that make possible such diverse discoveries, as the founding ideas of the American Republic, the Gauss-Riemann concept of the complex domain and Beethoven’s late string quartets.

The Universe is a wondrous, but not a strange place. As Nicholas of Cusa and G.W. Leibniz repeatedly emphasized, nothing exists or happens in the Universe that is not possible. It is the province of science, therefore, to discover what makes things possible. In so doing, the mind discovers not only the possibility of a particular thing, but it also discovers, and changes, the possibility of what it can discover about what is possible. Hence, Plato’s emphasis on the study of the above mentioned subjects. It is both a means to discover what makes these things possible and a pathway for the mind to discover how it is possible for it to discover what is possible, thereby increasing its power.

Proceed through the example of the mensuration of the line, surface and solid. As presented in earlier locations, each object is made possible by a principle that possess the power to produce it. The power to generate the line is different, and incommensurable with, the power that generates a square, which, in turn, is different and incommensurable with, the power to generate a solid. This, in itself, is a crucial discovery. But, the more important discovery comes when the next question is posed. Since all three distinct powers exist in the one Universe, what is it about the Universe that makes possible these three distinct powers?

The answer to this type of question does not lie in the particular nature of each discovery, but in the paradox that one universe produces all three. As Cusa put it in “On Learned Ignorance”:

“All our wisest and most divine teachers agree that visible things are truly images of invisible things and that from created things the Creator can be knowably seen as in a mirror and a metaphor. But the fact that spiritual matters (which are unattainable by us in themselves) are investigated metaphorically has its basis in what was said earlier. For all things have a certain comparative relation to one another, a relation which is nonetheless, hidden from us and incomprehensible to us), so that from out of all things there arises one universe and in this one maximum all things are this one. And although every image seems to be like its exemplar, nevertheless except for the Maximal Image (which is, in oneness of nature, the very thing which its Exemplar is) no image is so similar or equal to its exemplar that it cannot be infinitely more similar and equal…”

The square is bounded by lines, but those lines can only be produced from squares, not from lines alone. The action of doubling a square, as the Pythagoreans discovered, produces a certain harmony which they called geometric. Contained within that geometric series is a reflection of the harmony that doubles the cube, expressed as two geometric means between two extremes, instead of the one geometric mean expressed by the square. But, as the discoveries of Archytus and Menaechmus demonstrate, that “cubic” harmony, although reflected in the process of doubling the square, can only be constructed by a completely different process, that associated with the conic sections. Since the cube can generate a square and a square can generate a line, but not vice versa, all three powers can be understood as flowing from the higher principle of generation expressed by the conic sections. In other words, what makes all three powers possible is not manifest, sensually, in any of them. What makes them all possible is manifest only outside all lines, squares and cubes, in the principle of action exhibited by the conic sections.

Now, begins more fun. What makes the conic sections possible? To answer this question, one must first ferret out the contradictions within the domain of the conic sections. This will take us directly to Gauss’ discovery of the complex domain.

While Greek culture made significant advances in this direction, as exemplified by Apollonius’ Conics, the most significant advance was made by Kepler’s discovery of the projective relationship among the conic sections.

To grasp this, first think of the conic sections, as Apollonius did, as the curves produced by a plane cutting a set of cones joined at their apexes. A plane cutting the lower cone perpendicular to its axis will generate a circle. With the slightest tilt, that circle becomes an ellipse. As the plane’s tilt becomes parallel to the side of the cone, that ellipse becomes a parabola. With the slightest additional tilt, the plane now intersects both cones, forming an hyperbola. The top cone was sitting there all along, but didn’t come into play, until the hyperbola was formed.

From the standpoint of the visual appearance of the cone, all four conic sections are formed by one continuous motion of a plane intersecting with the cones. However, nothing can be discovered from this about what makes this conic manifold possible, unless the cognitive paradoxes, that reside “beyond the finite” are brought more sharply into view, metaphorically.

To do this, Kepler applied the method Cusa states in “On Learned Ignorance”:

“But since from the preceding points it is evident that the unqualifiedly Maximum cannot be any of the things which we either know or conceive: when we set out to investigate the Maximum metaphorically, we must leap beyond simple likeness. For since all mathematicals are finite and otherwise could not even be imagined; if we want to use finite things as a way for ascending to the unqualifiedly Maximum, we must first consider finite mathematical figures together with their characteristics and relations. Next, we must apply these relations, in a transformed way, to corresponding infinite mathematical figures. Thirdly, we must thereafter in a still more highly transformed way, apply the relations of these infinite figures to the simple Infinite, which is altogether independent even of all figures. At this point our ignorance will be taught incomprehensibly how we are to think more correctly and truly about the Most High as we grope by means of metaphor.”

Kepler’s interest in discovering the generating principle of the conic sections was not a matter of mathematical curiosity. His demonstration of the elliptical nature of the planetary orbits demanded a higher comprehension, beyond the simple mathematical relationships within and among the specific curves, of that universal principle (power) which made conic sections possible.

This required him, as Cusa indicated, to consider the finite relationships within and among the conic sections, from the standpoint of the infinite. By projecting the above cited process of a plane cutting a pair of cones onto one flat plane, Kepler brought out the infinite divide between the circle and the hyperbola. From the standpoint of Kepler’s projection, the hyperbola and circle were on opposite sides of the infinite. (See Figure 1.)

Figure 1

With this contradiction brought into view, the stage was set for Fermat, Huygens, Jakob and Johann Bernoulli and Leibniz to bring this paradox up to the point which demanded the discovery the complex domain by Gauss.

This was accomplished by focusing on the significance of this infinite divide between the circle and the hyperbola from the standpoint of the generation of Plato’s powers. On the one side, Jakob Bernoulli demonstrated that the circle, as a special case of an equiangular spiral, expressed the transcendental principle that generated all the so-called algebraic powers as a function of rotation. (See Figure 2.)

Figure 2

On the other side, Huygens demonstrated that the hyperbola expressed that same principle as a function of area and length. (See Figure 3.)

Figure 3

In this contradiction, Leibniz discovered something additional. While the circular principle expressed the transcendental number Pi, the exponential embodied by the hyperbola expressed a different transcendental number, that he called “b”, (later called “e” by Euler). (See Figure 4a and Figure 4b.)

Figure 4a

Figure 4b

Thus, both the circle and the hyperbola expressed, in different ways, a principle that had the power to produce all algebraic powers. Each expressed that power with respect to a different transcendental magnitude. An infinite gap lay between them. The question now posed anew was, what universal principle embodied the higher power that had the potential to generate both distinct transcendentals?

For Leibniz, as for Kepler earlier, this question was not posed as a formal mathematical curiosity. His and Johann Bernoulli’s joint discovery of the catenary demonstrated that the “frozen motion” of the hanging chain, expressed as a physical principle the simultaneous unity of both the trigonometric and exponential transcendentals. (See Figure 5a and Figure 5b.) The catenary, therefore, was the physical expression of a still yet undiscovered domain, that possessed the potential to generate all such transcendental magnitudes.

Figure 5a

Figure 5b

Leibniz understood that this higher domain existed outside the boundaries of the senses. Like all universal principles it could only be known with the mind, and so he referred to it as “imaginary” (not, as Euler would later say, “impossible”). This domain produced artifacts such as the ?-1, which posed a paradox because nothing within the known world could produce a magnitude, which when squared produced -1. Leibniz called ?-1, “a fine and wonderful recourse of the divine spirit, almost an amphibian, somewhere between being and non-being.”

The paradox remains regardless of whether one generates the powers by the spiral or the hyperbola. In the case of the spiral, successive angular rotation produces corresponding increases in the length of the radii of the spiral. The lengths increase by the power that corresponds to the how much the angle of rotation is increased. For example, if the rotation doubles, the length of radius is squared. If the rotation is tripled, the length of the radius is cubed. If the direction of the rotation is reversed, the length of the radii decrease, by the power equivalent to amount of rotation.

Similarly with the hyperbola. Equal areas between the hyperbola and the asymptote correspond to geometric increases in length along the asymptote. Thus, if the area is increased by two, the corresponding length along the asymptote is squared. If the area is increased by three, the corresponding length is cubed, etc. If the area is reduced by half, the corresponding length is reduced by the square root, etc.

So, in the hyperbola the areas change arithmetically while the lengths change geometrically. For the spiral, the angles change arithmetically while the lengths change geometrically. The angles of the spiral, and the areas for the hyperbola, were called by Huygens, Leibniz, and Bernoulli, logarithms.

The paradox posed by Leibniz was this: Since increases or decreases in the logarithms always produce a positive length, “what is the logarithm of a negative number?” or, in other words, what has the power to produce the ?-1.

This provoked a dispute with Johann Bernoulli. Bernoulli maintained that the logarithms of negative numbers were the same as the logarithms of positive numbers. For example, he considered 0 to be the logarithm of 1 and -1, just as 1 and -1 are both square roots of 1. Leibniz, on the other hand, recognized that the same action could not produce 1 and -1.

For Leibniz, this matter could not be resolved within the existing domain of accepted mathematical formalism, just as Gauss would demonstrate in his investigation of the fundamental theorem of algebra. The logarithms of negative numbers, Leibniz insisted, had to exist in a domain beyond the visible, i.e., the “imaginary” (not “impossible”). However, Leibniz was unable to complete this work and it wasn’t until Gauss developed his concept of the complex domain, that the full implications of Leibniz’ conjecture were resolved.

In the intervening period, Euler, commenting on the dispute between Leibniz and Bernoulli, developed a formal demonstration that indicated Leibniz, not Bernoulli was correct concerning the logarithms of negative numbers. Out of this came Euler’s famous identity, e^Pi?-1 – 1 = 0, a formula that has been used to torture students and brainwash potential thinkers ever since. For Euler, this was merely a formalism that has no real meaning other than the successful manipulation of symbols according to a regular set of rules. Countless victims have been brainwashed trying to find a meaning in this formalism within the formal mathematical domain. This is not possible, because the ?-1 is not possible in the formal mathematical domain of Euler, no matter how many times he refers to it.

Nevertheless, if looked at from the standpoint of Leibniz, Huygens, and Gauss, we can remove the mysticism associated with Euler’s identity and, using Cusa’s method of transforming the finite into the infinite, bring the matter clearly into view.

In the accompanying figure, the alternating areas of blue and yellow are all unit areas. Moving to the right, equal areas correspond to the logarithms that produce increasing powers of “e”. For example, beginning at 1, (where the logarithm is 0 because no area has been swept out) moving one unit area to the right increases the length from 1 to e. Moving another unit area increases the logarithm of 1 to 2 and the length from e to e². Halving the area between 1 and e produces the length ?e or e^1/2.

When moving left from 1, the principle of equal areas is maintained, but in the opposite direction. The lengths produced by these areas are the inverses of those produced by moving to the right. For example, moving one unit area to the left produces the length 1/e. Moving two unit areas left produces 1/e², etc.

The paradox to which Leibniz referred emerges when one tries to think how the hyperbola can produce a logarithm of a negative number. As is evident from the diagram, moving to right increases the lengths geometrically, while moving to the left decreases them. But because of the asymptotic nature of the hyperbola, the areas can never produce a length on the other side of 0.

As can be seen from the diagram, -1 is accessible, but only if the action detaches from the hyperbola and moves along the pathway around the circle. That is, to produce a logarithm of a negative number, we have to cross Kepler’s infinite boundary between the hyperbola and the circle! Half way around the circle will produce a length of -1. Dividing that action in half will, therefore, produce the action that corresponds to ?-1. Thus the logarithm of -1 can be thought of as a function of Pi and ?-1.

This matter cannot be resolved except from the standpoint of Gauss’ concept of the complex domain. Moving left and right within the domain of the hyperbola yields negative logarithms, but not the logarithms of negative numbers. Consequently, a higher concept that goes beyond simple back and forth action is required. This is exactly what Gauss specified as his complex domain.

As stated in his second treatise on biquadratic residues,: “Positive and negative numbers can be used only where the entity counted possesses an opposite, such that the unification of the two can be considered as equivalent to their dissolution. Judged precisely, this precondition is fulfilled only where relations between pairs of objects are the things counted, rather than substances (i.e. individually conceived objects). In this way we postulate that objects are ordered in some definite way into a series, for example A, B, C, D, … where the relation of A to B can be considered as identical to the relation of B to C and so forth. Here the concept of opposite consists of nothing else but interchanging the members of the relation, so that if the relation of (or transition from) A to B is taken as +1, then the relation of B to A must be represented by -1. Insofar as the series is unbounded in both directions, each real whole number represents the relation of an arbitrarily chosen member, taken as origin, to some determinate other member in the series.

“Suppose however the objects are of such a nature that they cannot be ordered in a single series, even if unbounded in both directions, but can only be ordered in a series of series, or in other words form a manifold of two dimensions; if the relation of one series to another or the transition from one series to another occurs in a similar manner as we earlier described for the transition from a member of one series to another member of the same series, then in order to measure the transition from one member of the system to another we shall require in addition to the already introduced units +1 and -1 two additional, opposite units +i and -i. Clearly we must also postulate that the unit i always signifies the transition from a given member to a determined member of the immediately adjacent series. In this manner the system will be doubly ordered into a series of series.”

In our diagram, the hyperbola is determining the action in the domain of logarithms of positive numbers, while the circle is generating action in the “imaginary” domain where the logarithms of negative numbers reside. If one mentally rotates the hyperbola perpendicular to the circle, as is its orientation within the cone, it would no longer be visible in our diagram. From this view, the hyperbola becomes, “imaginary” and the circle, “real”.

The complex domain is neither the domain of the “imaginary”, nor the “real”. It is the domain of possibility ( potential or power). As Riemann noted it is the efficient metaphor from which emerge, “a harmony and regularity that otherwise would remain hidden.”

To see this, look again at the harmony presented in the last installment. (See Figure 6, 7, 8, 9.)

When the catenary is expressed in the complex domain, the hyperbola and the circle (ellipses) are not on opposite sides of the infinite, but reside together, as a unified network of orthogonal least- action pathways within the complex domain.

If you listen carefully, you just might here, in these hidden harmonies, echos of Beethoven’s late string quartets.

TRANSCENDENTAL HARMONIES

Discoveries indicating the existence of what Gauss would later call the complex domain began with Pythagoras and his followers in the 6th Century B.C, These discoveries, which include the ratios of musical intervals, the doubling of the line, square and cube, the five regular solids, and many others, demonstrated that universal principles expressed themselves in the shadow world of the senses by harmonic proportions. Yet, in all cases, this harmony was never complete. There was always some small discrepancy, some paradoxical dissonance, that indicated a still undiscovered principle. This is why Pythagoras called geometry “science or inquiry”, and, according to Proclus, he thought that each discovery, “sets up a platform to ascend by, and lifts the soul on high instead of allowing it to go down among sensible objects and so become subservient to the common needs of this mortal life.”

The most persistent of the dissonances recognized by the Pythagoreans were not resolved until nearly 2500 years later, when, Bernhard Riemann, in his 1851 doctoral dissertation, noted that in Gauss’ domain of complex magnitudes, “a harmony and regularity emerge that otherwise remains hidden.”

To discover these otherwise hidden harmonies, we must first take a closer look at some paradigmatic discoveries in which the dissonances arise:

Pythagoras discovered that the concordant musical intervals corresponded to the proportions, 2:1, 3:2, 4:3, if produced by a straight vibrating string. These ratios produced the intervals known as the octave, fifth and fourth, respectively. More importantly, the Pythagoreans also discovered that if these proportions are simply extended, a discrepancy emerged called the Pythagorean comma.(See Fred Haight Pedagogy.) However, ideas are conveyed by the human voice singing poetry, not vibrating strings. The comma, therefore, is not a mere deficiency. It is an indication that a higher principle exists, a principle that actually governs musical harmonies, but which cannot be derived from the manifold of vibrating strings. It can only be derived from the manifold that has come to be known as the well-tempered system of bel canto polyphony, to which many analogies can be drawn to the complex domain. (fn. 1.)

Similar harmonic proportions are expressed by the principles governing the extension of a line, square and cube. Extension of a line produces relationships that the Pythagoreans called “arithmetic”, which correspond to the musical interval of a fifth. Extension of a square produces relationships called by the Pythagoreans, “geometric”, which correspond to the Lydian musical interval. While the arithmetic and geometric are harmonic within their own individual domain, together they form a dissonance, expressed as the incommensurability between arithmetic and geometric magnitudes. That dissonance indicates, as Plato noted, that the line and square were produced by principles of different “powers”.

The extension of the cube produces a third, higher, power, that cannot be generated by the line or square. Nevertheless, this power is expressed in the lower domain of squares by two geometric means between two extremes. But, as the discoveries of, most notably, Archytus and Menaechmus, showed, the construction of the magnitudes of this third power, cannot be generated by the squares among whose shadows it dwells. This cubic power is only generated by a higher form of curvature, such as that associated with conic sections and the torus.

Plato understood that the extension of line, square and cube denoted a succession of distinct higher powers. Leibniz would later discover an even higher principle that transcended all such powers. He called this transcendental principle, “exponential” or, inversely, “logarithmic”, the significance of which will be made more clear below.

Another class of harmonic proportions investigated by Pythagoras and his followers was associated with the five regular solids and the constructability of the regular polygons. The regular solids and constructable polygons were artifacts produced by the harmonic divisions of the sphere and circle. However, these harmonic divisions are bounded. There are only five regular divisions of the sphere, and, at least as far as the Pythagoreans were concerned, the constructable polygons were limited to the triangle, square, pentagon and certain combinations of the same. (fn.2.) The boundaries confronted by the divisions of the sphere and circle express a dissonance with respect to the harmonies governing those divisions.

This general class of principles, that is those associated with the divisions of the sphere and circle also comprise a class of transcendentals called “trigonometric”.

The unity between these two classes of transcendentals exemplifies the otherwise hidden harmony to which Riemann refers in his dissertation.

The first step toward the elaboration of this unity was taken by Nicholas of Cusa, who, citing Pythagoras, recognized that all universal principles expressed themselves harmonically in the domain of the senses. But, Cusa emphasized that these harmonies could only be expressed by the transcendental magnitudes typified by the dissonances identified in the above examples. Cusa, thus presented, the paradoxical proposition that the art of science is to seek out the dissonances and discover the transcendental principle that harmonizes them.

Johannes Kepler, applying Cusa’s insight, provided the first crucial experimental demonstration that physical principles could only be known through this transcendental harmony. This begins with his discovery of the harmonic correspondence between the five regular solids and the approximate orbits of the six visible planets, the discovery of which, Kepler states, depended on Cusa’s emphasis of the dissonance between the curved (spherical) and the straight (planar). Kepler’s further discovery of the eccentricity of the planetary orbits expressed another harmony through dissonance. Unlike a circular orbit, the regular divisions of an eccentric are dependent not on the angle, but on the sine of the angle, which is transcendental to the angle. Additionally, Kepler showed that the harmonic relationships among the orbital eccentricities of all the planets are dependent, not on the simple harmonies of the vibrating string, but on the dissonances indicated by the Pythagorean comma. (See “How Gauss Determined the Orbit of Ceres”, Summer 1998 Fidelio, and earlier installments of “Riemann for Anti-Dummies”.)

Fermat’s proof that the principle of least-time, not shortest distance, governed the propagation of light, is another experimental demonstration of physical action that is dependent not on the equality of angles, but on the proportionality of the sine.

In sum, the discoveries of Kepler and Fermat demonstrate that harmonic relationships in the physical universe are, as Cusa indicated, not expressible by precisely calculable numbers, but only by transcendental quantities a polyphony of dissonances.

The Leibniz-Bernoulli collaborative investigations into the principle governing the hanging chain, provide the crucial step to Riemann’s assertion.

As detailed in other locations, Bernoulli applying the principles of Leibniz’ calculus, demonstrated that the physical principle that determined the shape of the hanging chain was expressed by a proportionality of the sines of the angles formed by the chain and the physical singularity located at the chain’s lowest point. (See figure 1.)

On the other hand, Leibniz demonstrated that this same physical principle was also expressed as an exponential function. (See figure 2.)

Thus, the catenary expresses a unifying physical principle between what had appeared to be two different classes of transcendentals: the trigonometric and exponential. That unity, as Riemann indicates, only fully emerges when seen from the standpoint of Gauss’ complex domain.

The means to discover that harmonic unity, as in a musical composition, is by inversion.

Remember that the exponential and trigonometric functions first emerged as dissonances embedded in the harmonic relationships among objects in the visible domain. Now, think of those objects as artifacts of the dissonances, instead of the dissonances as artifacts of the objects.

For example, think of the circle as an artifact of the trigonometric transcendentals, and the line, square and cube, as artifacts of the transcendental exponential function. (See animation 1 and animation 2.)

This poses the difficulty of forcing the mind, as Cusa insists, away from the simple harmonic proportions among objects of visible space, to the transcendental harmonic proportions among the principles that generate them.

If we use the principle of the catenary as a pivot, we can present, at least in an intuitive form, the harmony of which Riemann speaks. A more complete demonstration will be left to future pedagogicals and to the oral discussions that this installment will undoubtedly provoke.

As previously noted, the catenary expresses both the trigonometric and the exponential functions. Thus, the catenary as the principle of physical least-action, subsumes both the principle of constant length (circle) and constant area (hyperbolic). (See figure 4.)

To this Leibniz added a new crucial conception: the exponential is the curve that embodies the principle of self-similar change. (See figure 5.) This led Leibniz to discover a new transcendental number that he denoted by the letter “b”. (Euler later derived the same quantity from formal algebra and denoted it by the letter “e” which is used today. It is typical of today’s academic frauds that this discovery is attributed to Euler’s formalism, instead of Leibniz’ Socratic idea.)

Figure 5

We have already seen how the hyperbola is generated by the exponential functions derived from the catenary. But, the exponential also generates the circle when the circle is thought of, as it should be, as a special case of an exponential spiral. Keep in mind Kepler’s projective relationship among the conic sections. (See Riemann for Anti-Dummies Part 33.) For Kepler the circle and the hyperbola were at opposite extremes of one manifold, and as such embody a common principle of generation. But, in that projective relationship, there was a discontinuous gap, a dissonance, between the hyperbola and the circle, giving the appearance that the hyperbola was on the “other side of the infinite” from the circle. Only in the complex domain of Gauss and Riemann does that gap disappear and that common generating principle harmonically expressed.

Since both the circle and the hyperbola are generated by the common principle expressed by the exponential, the trigonometric and hyperbolic functions can be represented as complex functions. Riemann created a concept of complex functions as transformations that produce manifolds of action, which in turn produce least-action pathways within that manifold. The study of complex functions formed the basis of Riemann’s work on algebraic, hypergeometric and abelian functions, which will be elaborated in future installments. As a precondition to that deeper study, we provide the reader with an intuitive view of the “otherwise hidden harmony and regularity” that emerges there.

Figures 6, 7, 8, 9, illustrate the complex mappings of the sine cosine, hyperbolic sine and hyperbolic cosine. As can be seen, all four functions express as artifacts, not one hyperbola or circle, but a system of orthogonal hyperbolas and circles.

Figures 10 and 11, and figures 12 and 13 illustrate surfaces constructed by the complex sine, cosine, hyperbolic sine and hyperbolic cosine. In the visible domain the circle is closed and periodic, while the hyperbola is infinite. Yet, when viewed from the standpoint of the complex domain, both are periodic. The shape of the curves rising from the surface, in both cases, are catenaries!

And, this is only the beginning.

NOTES

1. The analogy between well-tempered polyphony and the complex domain is most directly seen in the late quartets of Beethoven. There the characteristic half-step boundaries between neighboring keys and modes are transformed. Just as a solid is bounded by surfaces and a surface is bounded by lines, Beethoven transforms the keys and modes from the bounded to the boundaries of a “musical solid”.

2. It was one of Gauss’ earliest discoveries of the complex domain that the constructable polygons included the 17-gon and all polygons with the prime number of sides of the form 2^{2^n} + 1.

3. For generations students have been brainwashed by the Euler’s mystical algebraic derivation of the unity between the exponential and the trigonometric. The algebraic form of the circle as the curve of constant length is x² + y² = 1, where x and y are the legs of a right triangle. The algebraic expression of the hyperbola is x² – y² = 1. When factored algebraically the circle yields, (x + y?-1)(x – y?-1), while the hyperbola yields (x + y)(x – y).

Riemann for Anti-Dummies Part 33

HYPERBOLIC FUNCTIONS – A FUGUE ACROSS 25 CENTURIES

When the Delians, circa 370 B.C., suffering the ravages of a plague, were directed by an oracle to increase the size of their temple’s altar, Plato admonished them to disregard all magical interpretations of the oracle’s demand and concentrate on solving the problem of doubling the cube. This is one of the earliest accounts of the significance of pedagogical, or spiritual, exercises for economics.

Some crises, such as the one currently facing humanity, require a degree of concentration on paradoxes that outlasts one human lifetime. Fortunately, mankind is endowed with what LaRouche has called, “super-genes,” which provide the individual the capacity for higher powers of concentration, by bringing the efforts of generations past into the present. Exemplary is the case of Bernhard Riemann’s 1854 habilitation lecture, On the Hypotheses that Underlie the Foundations of Geometry, in which Riemann speaks of a darkness that had shrouded human thought from Euclid to Legendre. After more than 2,000 thousand years of concentration on the matter, Riemann, standing on the shoulders of his teacher, Carl F. Gauss, lifted that darkness, by developing what he called, “a general concept of multiply-extended magnitude.”

Riemann’s concept extended the breakthroughs already put forward by Gauss, beginning with his 1799 dissertation on the fundamental theorem of algebra. Like its predecessor, it is a devastating refutation of the “ivory tower” methods of Euler, Lagrange, et al. that dominate the thinking of most of the population today, just as it dominated the minds of the Delians and the other unfortunate Greeks of Plato’s time. Recognizing that all problems of society were ultimately subjective, Plato prescribed (in The Republic) that mastery of pedagogical exercises, (in the domain of music, geometry, arithmetic, and astronomy) be a prerequisite for political leadership. Only if leaders developed the capacity to free themselves, and then others, from this wrong-headedness, could crises, like the one facing us (or that which faced the Delians), be vanquished.

These exercises accustom the mind to shift its attention from the shadows of sense perception, to the discovery of knowable, but unseen truths, that are reflected to us as paradoxes in the domain of the senses. The process is never-ending. With each new discovery, new paradoxes are brought to the surface, which provoke still further discoveries, producing an ever greater concentration of the requisite quality of mind that produced the discovery in the first place.

Doubling of the Line, Square, and Cube

Such is the context for concentrating on the 2,500-year investigation of the paradoxes initially posed by the problem of doubling the line, square, and cube. These objects appear, visually, to be similar. The square is made from lines, while the cube is made from squares. Yet, when subjected to an action, such as doubling, it becomes evident that while these objects appear visibly similar, their principle of generation is vastly different.

The Pythagoreans, who learned from the Egyptians, reportedly, were the first Greeks to investigate this paradox. Recognizing that these visibly similar, but knowably different, objects were all contained in one universe, they sought a unifying principle that underlay the generation of all three. That unifying principle could not be directly observed, but its existence could be known, through its expression, as a paradox, lurking among the shadows that were seen.

Nearly 80 years before Plato’s rebuke of the Delians, Hippocrates of Chios offered an insight based on the Pythagorean principle of the connection among music, arithmetic, and geometry. The Pythagoreans had recognized relationships among musical intervals, which they called: the arithmetic and the geometric. The arithmetic mean is found when three numbers are related by a common difference: b – a = c – b. For example, 3 is the arithmetic mean between 1 and 5. (see Figure 1a).

The geometric mean is when three numbers are in constant proportion, a:b::b:c. For example, 2:4::4:8. (see Figure 1b ).

Hippocrates recognized that the arithmetic relationship is expressed by the intervals formed when lines are added, and that the geometric is expressed by the intervals when squares, or more generally, areas, are added. The formation of solid figures, being of a still higher power, did not correspond directly to any of these musical relationships. Nevertheless, the shadow cast by the doubling of the cube, expressed a relationship that corresponded to finding two geometric means between two extremes (see Figure 1c).

Plato, in the Timaeus, explains the significance of Hippocrates’ insight:

“Now that which is created is of necessity corporeal, and also visible and tangible…. But it is not possible that two things alone be joined without a third; for in between there must needs be some bond joining the two…. Now if the body of the All had had to come into being as a plane surface, having no depth, one mean would have sufficed to bind together both itself and its fellow-terms; but now it is otherwise, for it behooved it to be solid in shape, and what brings solids into harmony is never one mean, but always two.”

In the Epinomis, Plato says of the investigations of the arithmetic and geometric means, “a divine and marvelous thing it is to those who contemplate it and reflect how the whole of nature is impressed with species and kind according to each proportion as power…. To the man who pursues his studies in the proper way, all geometric constructions, all systems of numbers, all duly constituted melodic progressions, the single ordered scheme of all celestial revolutions, should disclose themselves, and disclose themselves they will, if, as I say, a man pursues his studies aright with his mind’s eye fixed on their single end. As such a man reflects, he will receive the revelation of a single bond of natural interconnection between all these problems. If such matters are handled in any other spirit, a man, as I am saying, will need to invoke his luck. We may rest assured that without these qualifications the happy will not make their appearance in any society; this is the method, this the pabulum, these the studies demanded; hard or easy, this is the road we must tread.”

While the initial reported reaction to Hippocrates was that he had turned one impossible puzzle into another, others saw his insight as a flank. If the construction of two means between two extremes could be carried out among the shadows, the result could be applied to double the cube. Plato’s collaborator, Archytas of Tarentum, supplied a solution by his famous construction involving a cylinder, torus, and cone. (See Figure) This demonstrated that the required construction could only be carried out, not in the flat domain of the shadows, but in the higher domain of the curved surfaces. Archytas’ result is consistent with the discovery of the Pythagoreans, Theatetus, and Plato, of the construction of the five regular solids from the sphere.

Menaechmus’ Discovery

Plato’s student, Menaechmus, supplied a further discovery, by demonstrating that curves generated from cones possessed the power to produce two means between two extremes. As the accompanying diagrams illustrate, the parabola possesses the characteristic of one mean between two extremes, while the hyperbola embraces two (see Figures 2a and Figure 2b, and Animation 1a and Animation 1b).

Menaechmus showed that the intersection of an hyperbola and a parabola produces the result of placing two means between two extremes (Figure 3).

Embedded in the discoveries of Archytas and Menaechmus was a principle that would not fully blossom until 2,200 years later, with the discoveries of Riemann and Gauss. Archytas’ solution depended on a characteristic possessed by the curve formed by the intersection of the cylinder and torus. This curve could not be drawn on a flat plane, because it curved in two directions. Gauss would later define this characteristic as “negative” curvature.(Figure 4).

However, Menaechmus’ construction using a parabola and hyperbola, is carried out entirely in the flat domain of the shadows. Nonetheless, for reasons that would not become apparent until Gottfried Wilhelm Leibniz in the 17th Century, Menaechmus’ solution worked because it contained this same principle of negative curvature as did Archytas’.

Because of the lack of extant original writings, it is difficult to know how conscious these ancient Greek investigators were of the principle which Gauss would call negative curvature. What is known, is that these Greeks knew that the principle that determined action in the physical universe, was a higher principle than that which dominated the flat world of areas. The principles governing solid objects, thus, depended on curves, generated by a higher type of action in space, which, when projected onto the lower domain of a plane, exhibited the capacity of putting two means between two extremes. These curves combined the arithmetic and the geometric into a One. When this principle was applied in the higher domain of solid objects, it produced the experimentally validatable result.

This demonstrates, as Plato makes clear, not simply a principle governing the physical realm, but the multiply-connected relationship between the spiritual and the material dimensions of the universe; hence the appropriateness of “pedagogical,” or “spiritual exercises.”

Kepler’s Study of Conic Sections

The next significant step was accomplished by Johannes Kepler, who established modern physical science as an extension of these ancient Greek discoveries as those discoveries were re-discovered by Nicolaus of Cusa, Luca Pacioli, and Leonardo da Vinci. Kepler, citing Cusa, whom he called “divine,” placed particular importance on the difference between the curved (geometric) and the straight (arithmetic).

“But after all, why were the distinctions between curved and straight, and the nobility of a curve, among God’s intentions when he displayed the universe? Why indeed? Unless because by a most perfect Creator it was absolutely necessary that a most beautiful work should be produced,” Kepler wrote in the Mysterium Cosmographicum.

As part of his astronomical research, Kepler mastered the compilation of Greek discoveries on these higher curves contained in Apollonius’ {Conics.} As a result of his investigation of refraction of light, Kepler reports a revolutionary new concept of conic sections. For the first time, Kepler considered the conic sections as one projective manifold:

“[T]here exists among these lines the following order by reason of their properties: It passes from the straight line through an infinity of hyperbolas to the parabola, and thence through an infinity of ellipses to the circle. Thus the parabola has on one side two things infinite in nature, the hyperbola and the straight line, the ellipse and the circle. For it is also infinite, but assumes a limitation from the other side…. Therefore, the opposite limits are the circle and the straight line: The former is pure curvedness, the latter pure straightness. The hyperbola, parabola, and the ellipse are placed in between, and participate in the straight and the curved, the parabola equally, the hyperbola in more of the straightness, and the ellipse in more of the curvedness.” (See Figure 5 and Animation 2.)

Animation 2

Of significance for this discussion is the discontinuity revealed by this projection between the parabola and the hyperbola. The hyperbola stands on the other side of the infinite, so to speak, from the ellipse and the circle, while the parabola has one side toward the infinite and the other toward the finite.

From Fermat to Gauss

The significance of this infinite boundary begins to become clear from the standpoint of Pierre de Fermat’s complete re-working of Apollonius’ Conics and the subsequent development of the calculus by Leibniz and Jean Bernoulli, with a crucial contribution supplied by Christian Huyghens.

Huyghens recognized that the curved and the straight expressed themselves in the hyperbola differently than in the other conic sections. His insight was based on the same principle recognized by Menaechmus, that the hyperbola, when projected onto a plane, was formed by a series of rectangles whose area was always equal. As one of the sides of each rectangle got longer, the other side got inversely smaller. Huyghens focused his attention on the area bounded by the hyperbola and the asymptote, which is the area formed by an ever-changing rectangle whose area is always the same (Figure 6). Areas between the hyperbola and the asymptote, formed by rectangles whose sides are in proportion, are equal. Consequently, as the diagram illustrates, those sections of the hyperbola, formed as the distance along the asymptote from the center increases geometrically, are equal. Thus, as the areas increase arithmetically, the lengths along the asymptote increase geometrically. Don’t miss the irony of this inversion: In the hyperbola, the (geometric) areas grow arithmetically, while the (arithmetic) lengths grow geometrically!

As has been presented in previous installments of this series, this combined relationship of the arithmetic with the geometric was discovered by Leibniz to be expressed by the physical principle of the catenary. Leibniz demonstrated that the catenary was formed by a curve, which he called “logarithmic,” today known as the “exponential.” This curve is formed such that the horizontal change is arithmetic, while the vertical change is geometric. The catenary, Leibniz demonstrated, is the arithmetic mean between two such “logarithmic” curves (Figure 7).

From here we are led directly into the discovery of Gauss and Riemann through Leibniz’ and Bernoulli’s other catenary-related discovery: The relationship of the catenary to the hyperbola(1). This relationship is formed from Huyghens’ discovery. The equal hyperbolic areas define certain points along the hyperbola, that are “projected” onto the axis of the hyperbola, by perpendicular lines drawn from axis to those points. These projections produce lengths along the axis, that are the same lengths that, as Leibniz showed, produced the catenary! (See Figure 8a, Figure 8b, Figure 8c and Figure 8d.)

The implications of this discovery become even more clear when viewed from the standpoint of Gauss’ investigation of curved surfaces that arose out of his earlier work on the fundamental theorem of algebra, geodesy, astronomy, and biquadratic residues. To complete this discussion, focus on Gauss’ extension of the investigations of curves, into the investigation of the surfaces which contain them. Surfaces that contained curves with the characteristics of the hyperbola or catenary, Gauss called “negatively” curved, while surfaces that were formed by curves with the characteristics of circles and ellipses, he called “positively” curved(2). (See Figures 9.)

Now think back over this 2,500-year fugue. The principle underlying the constructions of Archytas and Menaechmus; the discontinuity expressed by the infinite boundary between the hyperbola and parabola; the inversion of the geometric and arithmetic in the hyperbola: From Gauss’ perspective, these all reflect a transformation between negative and positive curvature.

Thus, to investigate action in the physical universe, it is necessary to extend the inquiry from simple extension to curvature and from simple curves to the surfaces that contain them. This, as will be developed in future installments, can only be done from the standpoint of Gauss and Riemann’s complex domain.

NOTES

1. It should be noted that this discovery has been the victim of such a widespread pogrom initiated by Euler, Lagrange, and carried into the 20th Century by Felix Klein et al., that the mere discussion of it with anyone exposed to an academic mathematics education, is likely to provoke severe outbreaks of anxiety.

2. The reason for the names “negative” and “positive” will be discussed in a future installment.

Riemann for Anti-Dummies Part 28

BRINGING THE INVISIBLE TO THE SURFACE

When Carl Friedrich Gauss, writing to his former classmate Wolfgang Bolyai in 1798, criticized the state of contemporary mathematics for its “shallowness”, he was speaking literally – and, not only about his time, but also of ours. Then, as now, it had become popular for the academics to ignore, and even ridicule, any effort to search for universal physical principles, restricting the province of scientific inquiry to the, seemingly more practical task, of describing only what’s on the surface. Ironically, as Gauss demonstrated in his 1799 doctoral dissertation on the fundamental theorem of algebra, what’s on the surface, is revealed only if one knows, what’s underneath.

Gauss’ method was an ancient one, made famous in Plato’s metaphor of the cave, and given new potency by Johannes Kepler’s application of Nicholas of Cusa’s method of On Learned Ignorance. For them, the task of the scientist was to bring into view, the underlying physical principles, that could not be viewed directly-the unseen that guided the seen.

Take the illustrative case of Pierre de Fermat’s discovery of the principle, that refracted light follows the path of least time, instead of the path of least distance followed by reflected light. The principle of least-distance, is a principle that lies on the surface, and can be demonstrated in the visible domain. On the other hand, the principle of least-time, exists “behind”, so to speak, the visible, brought into view, only in the mind. On further reflection, it is clear, that the principle of least-time, was there all along, controlling, invisibly, the principle of least-distance. In Plato’s terms of reference, the principle of least-time is of a “higher power”, than the principle of least-distance.

Fermat’s discovery is a useful reference point for grasping Gauss’ concept of the complex domain. As Gauss himself stated, unequivocally, this is not Leonard Euler’s formal, superficial concept of “impossible” numbers (a fact ignored by virtually all of today’s mathematical “experts”). Rather, Gauss’ concept of the complex domain, like Fermat’s principle of least-time, brings to the surface, a principle that was there all along, but hidden from view.

As Gauss emphasized in his jubilee re-working of his 1799 dissertation, the concept of the complex domain is a “higher domain”, independent of all a priori concepts of space. Yet, it is a domain, “in which one cannot move without the use of language borrowed from spatial images.”

The issue for Gauss, as for Gottfried Leibniz, was to find a general principle, that characterized what had become known as “algebraic” magnitudes. These magnitudes, associated initially, with the extension of lines, squares, and cubes, all fell under Plato’s concept of “dunamais”, or “powers”.

Leibniz had shown, that while the domain of all “algebraic” magnitudes consisted of a succession of higher powers, the entire algebraic domain, was itself dominated by a domain of a still higher power, that Leibniz called, “transcendental”. The relationship of the lower domain of algebraic magnitudes, to the higher non-algebraic domain of transcendental magnitudes, is reflected in, what Jacob Bernoulli discovered about the equiangular spiral. (See Figure 1.)

Figure 1

Leibniz and Johann Bernoulli (Jakob’s brother) subsequently demonstrated that his higher, transcendental domain, exists not as a purely geometric principle, but originates from the physical action of a hanging chain, whose geometric shape Christaan Huygens called a catenary. (See Figure 2.) Thus, the physical universe itself demonstrates, that the “algebraic” magnitudes associated with extension, are not generated by extension. Rather, the algebraic magnitudes are generated from a physical principle that exists, beyond simple extension, in the higher, transcendental, domain.

Figure 2

Gauss, in his proofs of the fundamental theorem of algebra, showed that even though this transcendental physical principle was outside the visible domain, it nevertheless cast a shadow that could be made visible in what Gauss called the complex domain.

As indicated in “Gauss’ Declaration of Independence,” the discovery of a general principle for “algebraic” magnitudes was found, by looking through the “hole” represented by the square roots of negative numbers, which could appear as solutions to algebraic equations, but lacked any apparent physical meaning. For example, in the algebraic equation x² = 4, “x” signifies the side of a square whose area is 4, while, in the equation x² = -4, the “x” signifies the side of a square whose area is -4, an apparent impossibility. For the first case, it is simple to see, that a line whose length is 2 would be the side of the square whose area is 4. However, from the standpoint of the algebraic equation, a line whose length is -2, also produces the desired square.

At first glance, a line whose length is -2 seems as impossible as a square whose area is -4. Yet, if you draw a square of area 2, you will see that there are two diagonals, both of which have the power to produce a new square whose area is 4. These two magnitudes are distinguished from one another only by their direction, so one is denoted as 2 and the other as -2.

Now extend this investigation to the cube. In the algebraic equation x³ = 8, there appears to be only one number, 2 which satisfies the equation, and this number signifies the length of the edge of a cube whose volume is 8. This appears to be the only solution to this equation since -2x – 2x – 2 = -8.

The anomaly that there are two solutions, which appeared for the case of a quadratic equation, seems to disappear, in the case of the cube, for which there appears to be only one solution.

Not so fast. Look at another geometrical problem, that, when stated in algebraic terms, poses the same paradox–the trisection of an arbitrary angle. Like the doubling of the cube, Greek geometers could not find a means for equally trisecting an arbitrary angle, from the principle of circular action itself. The several methods discovered, (by Archimedes, Erathosthenes, and others), to find a general principle of trisecting an angle, were similar to those found, by Plato’s collaborators, for doubling the cube. That is, this magnitude could not be constructed using only a circle and a straight line, but it required the use of extended circular action, such as conical action.

But, trisecting an arbitrary angle presents another type of paradox which is not so evident in the problem of doubling the cube. To illustrate this, make the following experiment:

Draw a circle. For ease of illustration, mark off an angle of 60 degrees. It is clear that an angle of 20 degrees will trisect this angle equally. Now add one circular rotation to the 60 degree angle, making an angle of 420 degrees. It appears these two angles are essentially the same. But, when 420 is divided by 3 we get an angle of 140 degrees. Add another 360 degree rotation and we get to the angle of 780 degrees, which appears to be exactly the same as the angles of 60 and 420 degrees. Yet, when we divide 780 degrees by 3 we get 260 degrees. Keep this up, and you will see that the same pattern is repeated over and over again. (See Figure 3.)

Figure 3

Looked at from the domain of sense certainty, the angle of 60 degrees can be trisected by only one angle, that is, an angle of 20 degrees. Yet, when looked at beyond sense certainty, there are clearly three angles that “solve” the problem.

This illustrates another “hole” in the algebraic determination of magnitude. In the case of quadratic equations, there seems to be two solutions to each problem. In some cases, such x² = -4, those solutions seem to have a visible existence. While for the case, x² = -4, there are two solutions, 2?-1 and -2?-1, both of which seem to be “imaginary”, having no physical meaning. In the case of cubic equations, sometimes there are three visible solutions, such as in the case of trisecting an angle. Yet, in the case of doubling the cube, there appears to be only one visible solution, but two “imaginary” solutions, specifically: -1 – ?3?-1, -1 + ?3?-1. Biquadratic equations, (for example x⁴ = 16) , that seem to have no visible meaning themselves, have four solutions, two “real” (2 and -2) and two “imaginary” (2?-1 and -2?-1). Things get even more confused for algebraic magnitudes of still higher powers. This anomaly poses the question that Gauss resolved in his proof of what he called the fundamental theorem of algebra; that is: how many solutions are there for any algebraic equation?

The “shallow” minded mathematicians of Gauss’ day, such as Euler, Lagrange, and D’Alembert, took the superficial approach of asserting that any algebraic equation has as many solutions as it has powers, even if those solutions were “impossible”, such as the square roots of negative numbers. (This sophist’s argument is analogous to saying there is a difference between man and beast, but, this difference is meaningless.)

Gauss, in his 1799 dissertation, polemically exposed this fraud for the sophistry it was. “If someone would say a rectilinear equilateral right triangle is impossible, there will be nobody to deny that. But, if he intended to consider such an impossible triangle as a new species of triangles and to apply to it other qualities of triangles, would anyone refrain from laughing? That would be playing with words, or rather, misusing them.”

For, Gauss, no magnitude could be admitted, unless its principle of generation was demonstrated. For magnitudes associated with the square roots of negative numbers, that principle was the complex physical action of rotation combined with extension. Magnitudes generated by this complex action, Gauss called “complex numbers” in which each complex number denoted a quantity of combined rotational and extended action. The unit of action in Gauss’ complex domain is a circle, which is one rotation with an extension of unit length. The number 1 signifies one complete rotation, -1 one half a rotation, ?-1 one fourth a rotation, and -?-1 three fourths a rotation. (See Figure 4.)

Figure 4

These “shadows of shadows”, as he called them, were only a visible reflection of a still higher type of action, that was independent of all visible concepts of space. These higher forms of action, although invisible, could nevertheless be brought into view as a projection onto a surface.

Gauss’ approach is consistent with that employed by the circles of Plato’s Academy, as indicated by their use of the term “epiphanea” for surface, which comes from the same root as the word, “epiphany”. The concept indicated by the word “epiphanea” is, ” that on which something is brought into view”.

From this standpoint, Gauss demonstrated, in his 1799 dissertation, that the fundamental principle of generation of any algebraic equation, of no matter what power, could be brought into view, “epiphanied”, so to speak, as a surface in the complex domain. These surfaces were visible representations, not, as in the cases of lines, squares and cubes, of what the powers produced, but of the principle that produced the powers.

To construct these surfaces, Gauss went outside the simple visible representation of powers, such as squares and cubes, by seeking a more general form of powers, as exhibited in the equiangular spiral. (See Figure 5.) Here, the generation of a power, corresponds to the extension produced by an angular change. For example, the generation of square powers, corresponds to the extension that results from a doubling of the angle of rotation around the spiral.

Figure 5

The generation of cubed powers corresponds to the extension that results from tripling the angle of rotation. Thus, it is the principle of squaring that produces square magnitudes, and the principle of cubing that produces cubics. (See figure 6.)

Figure 6

For example, in Figure 7 , the complex number z is “squared” when the angle of rotation is doubled from x to 2x and the length squared from A to A². In doing this, the smaller circle maps twice onto the larger “squared” circle.

Figure 7

In Figure 8, the same principle is illustrated with respect to cubing. Here the angle x is tripled to 3x, and the length A is cubed to A³. In this case, the smaller circle maps three times onto the larger, “cubed” circle.

Figure 8

And so on for the higher powers. The fourth power maps the smaller circle four times onto the larger. The fifth power, five times, and so forth.

This gives a general principle that determines all algebraic powers, as, from this standpoint, all powers are reflected by the same action. The only thing that changes with each power, is the number of times that action occurs. Thus, each power is distinguished from the others, not by a particular magnitude, but by a topological characteristic.

In his doctoral dissertation, Gauss used this principle to generate surfaces that expressed the essential characteristic of powers in an even more fundamental way. Each rotation and extension, produced a characteristic right triangle. The vertical leg of that triangle is called the sine and the horizontal leg of that triangle is called the cosine. (See Figure 9.)

Figure 9

There is a cyclical relationship between the sine and cosine which is a function of the angle of rotation. When the angle is 0, the sine is 0 and the cosine is 1. When the angle is 90 degrees the sine is 1 and the cosine is 0. Looking at this relationship for an entire rotation, the sine goes from 0 to 1 to 0 to -1 to 0, while the cosine goes from 1 to 0 to -1 to 0 and back to 1. (See Figure 10)

Figure 10

In Figure 9, as z moves from 0 to 90 degrees, the sine of the angle varies from 0 to 1, but at the same time, the angle for z² goes from 0 to 180 degrees, and the sine of z² varies from 0 to 1 and back to 0. Then as z moves from 90 degrees to 180 degrees, the sine varies from 1 back to 0, but the angle for z² has moved from 180 degrees to 360 degrees, and its sine has varied from 0 to -1 to 0. Thus, in one half rotation for z, the sine of z² has varied from 0 to 1 to 0 to -1 to 0.

In his doctoral dissertation, Gauss represented this complex of actions as a surface. (See Figures 11, 12, 13.) Each point on the surface is determined so that its height above the flat plane, is equal to the distance from the center, times the sine of the angle of rotation, as that angle is increased by the effect of the power. In other words, the power of any point in the flat plane, is represented by the height of the surface above that point. Thus, as the numbers on the flat surface move outward from the center, the surface grows higher according to the power. At the same time, as the numbers rotate around the center, the sine will pass from positive to negative. Since the numbers on the surface are the powers of the numbers on the flat plane, the number of times the sine will change from positive to negative, depends on how much the power changes the angle (double for square powers, triple for cubics, etc.). Therefore, each surface will have as many “humps” as the equation has dimensions. Consequently, a quadratic equation will have two “humps” up and two “humps” down (Figure 11).

Figure 11

A cubic equation will have three “humps” up and three “humps” down. (Figure 12). A fourth degree equation four “humps” in each direction, (Figure 13), and so on.

Figure 12

Figure 13

Gauss specified the construction of two surfaces for each algebraic equation, one based on the variations of the sine and the other based on the variations of the cosine. (See figures 14a and 14b.)

Figure 14a

Figure 14b

Each of these surfaces will define definite curves where the surfaces intersect the flat plane. The number of curves will depend on the number of “humps” which in turn depend on the highest power. Since each of these surfaces will be rotated 90 degrees to each other, these curves will intersect each other, and the number of intersections, will correspond to the number of powers. (See figures 15a and 15b.) If the flat plane is considered to be 0, these intersections will correspond to the solutions, or “roots” of the equation. Thus, proving that an algebraic equation has as many roots as its highest power.

Figure 15a

Figure 15b

Step back and look at this work. These surfaces were produced, not from visible squares or cubes, but from the general principle of squaring, cubing, and higher powers. They represent, metaphorically, a principle that manifests itself physically, but cannot be seen. By projecting this principle, the general form of Plato’s powers, onto these complex surfaces, Gauss has brought the invisible into view, and made intelligible, something that is incomprehensible in the superficial world of algebraic formalism.

The effort to make intelligible the implications of the complex domain was a focus for Gauss throughout his life. Writing to his friend Hansen on December 11, 1825, Gauss said: “These investigations lead deeply into many others, I would even say, into the Metaphysics of the theory of space, and it is only with great difficulty can I tear myself away from the results that spring from it, as, for example, the true metaphysics of negative and complex numbers. The true sense of the square root of -1 stands before my mind fully alive, but it becomes very difficult to put it in words; I am always only able to give a vague image that floats in the air.”

It is here, that Riemann begins.

Riemann for Anti-Dummies Part 27

GAUSS’ DECLARATION OF INDEPENDENCE

In September 1798, after three years of self-directed study, C.F. Gauss, then 21 years old, left Goettingen University without a diploma. He returned to his native city of Brunswick to begin the composition of his “Disquisitiones Arithmeticae.” lacking any prospect of employment, he hoped to continue receiving his student stipend. After several months of living on credit, word came from the Duke that the stipend would continue, provided Gauss obtained his doctor of philosophy degree, a task Gauss thought a distraction and wished to postpone.

Nevertheless, he took the opportunity to produce a virtual declaration of independence from the stifling world of deductive mathematics, in the form of a written thesis submitted to the faculty of the University of Helmstedt, on a new proof of the fundamental theorem of algebra. Within months, he was granted his doctorate without even being required to appear for oral examination.

Describing his intention to his former classmate, Wolfgang Bolyai, Gauss wrote, “The title indicates quite definitely the purpose of the essay; only about a third of the whole, nevertheless, is used for this purpose, the remainder contains chiefly the history and a critique of works on the same subject by other mathematicians (viz. d’Alembert, Bougainville, Euler, de Foncenex, Lagrange, and the encyclopedists … which latter, however, will probably not be much pleased) besides many and varied comments on the shallowness which is so dominant in our present-day mathematics.”

In essence, Gauss was defending, and extending, a principle, that goes back to Plato, in which only physical action, not arbitrary assumptions, defines our notion of magnitude. Like Plato, Gauss also recognized it were not sufficient to simply state his discovery, without a polemical attack on the Aristotelean falsehoods that had become so popular among his contemporaries.

Looking back on his dissertation 50 years later, Gauss said, “The demonstration is presented using expressions borrowed from the geometry of position, for in this way, the greatest acuity and simplicity is obtained. Fundamentally, the essential content of the entire argument belongs to a higher domain, independent from space, (i.e., anti-Euclidean) in which abstract general concepts of magnitudes, are investigated as combinations of magnitudes connected by continuity, a domain, which, at present, is poorly developed, and in which one cannot move without the use of language borrowed from spatial images.”

It is the intention of this installment to provide a summary sketch of the history of this conception, and Gauss’ development of it. Because of the difficulties of this medium, it can not be exhaustive. Rather, it seeks to outline the steps which should form the basis for extended oral pedagogical dialogues, such as is already underway in various locations.

Multiply-Extended Magnitude

A physical concept of magnitude was already fully developed by those circles associated with Plato, expressed most explicitly in the Meno, Theatetus, and Timaeus dialogues. Plato and his circle demonstrated this concept, pedagogically, through the paradoxes that arise when considering the uniqueness of the five regular solids, and the related problems of doubling a line, square, and cube. As Plato emphasized, each species of action, generated a different species of magnitude. He denoted such magnitudes by the Greek term, “dunamais”, a term akin to Leibniz’ use of the word “kraft”, translated into English as “power”. That is, a linear magnitude has the “power” to double a line, while only a magnitude of a different species has the “power” to double the square, and a still different species has the “power” to double a cube. (See figures 1a, 1b and 1c). In Riemann’s language, these magnitudes are called, respectively, simply, doubly, and triply extended. Plato’s circle emphasized that magnitudes of lesser extension lacked the capacity to generate magnitudes of higher extension, creating, conceptually, a succession of “higher powers”.