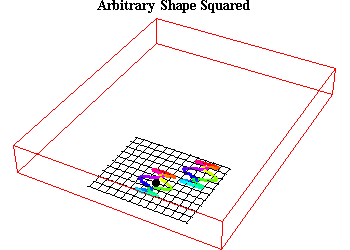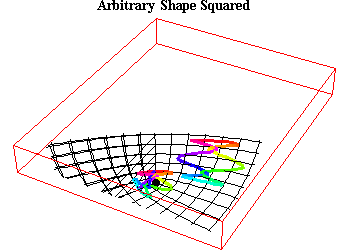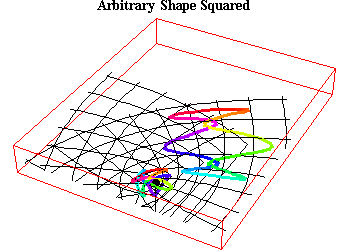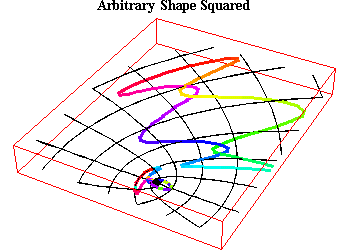
RIEMANNIAN SPHERICS
When Carl Friedrich Gauss repeatedly stated his conviction that Euclidean geometry was not true, his thoughts were connected to the pre-Euclidean science of the Pythagoreans and Plato. However Gauss’s “{anti}-Euclideanism” was not a mere restatement of its antecedent. Rather, Gauss, and later Riemann, sublimated the ancient Egyptian-Pythagorean science of “spherics” with a new spherics, that had been demanded by Cusa’s discovery of transcendental physical action, the development of Kepler’s discovery of the harmonics of elliptical planetary orbits, and Leibniz’s generalization of both, as the universal principle of least-action.
This is the vantage point from which to gain a firmer grasp of Riemann’s treatment of Abelian and hypergeometric functions.
The relevant characteristics of the Pythagorean concept of spherics are summarized in the Plato dialogue, named for the astronomer Timaeus, who, attributing the origin of his discourse to the testimony of wise men from more ancient times, recounts the nature and creation of the universe. Timaeus begins by noting that investigations of the created world must focus on the eternal universal principles from which it is patterned. Though “apprehensible by reason and thought,”, those principles are, of necessity, reflected in the world’s physical form. Accordingly, when speaking about the physical universe, Timaeus emphasizes, it is most important to distinguish between the original principles and their created copy, and one must be careful to recognize that a simple description of the latter cannot suffice for an explanation of the former.
“Accordingly, in dealing with a copy and its model, we must affirm that the accounts given will themselves be akin to the diverse objects which they serve to explain; those which deal with what is abiding and firm and discernible by the aid of thought will be abiding and unshakable; and in so far as it is possible and fitting for statements to be irrefutable and invincible, they must in no wise fall short thereof; whereas the accounts of that which is copied after the likeness of that model, and is itself a likeness, will be analogous thereof and possess likelihood; for as Being is to Becoming, so is Truth to Belief. Wherefore, Socrates, if in our treatment of a great host of matters regarding the Gods and the generation of the Universe we prove unable to give accounts that are always in all respects self-consistent and perfectly exact, be not thou surprised; rather we should be content if we can furnish accounts that are inferior to none in likelihood, remembering that both I who speak and you who judge are but human creatures, so that it becomes us to accept the likely account of these matters and forbear to search beyond it.” (29c-d)
Timaeus goes on to say that the Creator, being good, intended for that goodness to be reflected in the creation and so he endowed it with intelligence and soul, and brought it into existence as a self moving, self-subsisting living creature.
“He fashioned it to be One single Whole, compounded of all wholes, perfect and ageless and unailing. And he bestowed on it the shape which was befitting and akin. Now for that living creature which is designed to embrace within itself all living creatures, the fitting shape will be that which comprises within itself all the shapes there are; wherefore he wrought it into a round, in the shape of a sphere, equidistant in all directions from the center to extremities, which of all shapes is the most perfect and most self-similar, since he deemed that the similar is infinitely fairer than the dissimilar….
“Such then was the reasoning of the ever-existing God concerning the god which was one day to become existent, whereby He made it smooth and even and equal on all sides from the center, a whole and perfect body compounded of perfect bodies, and in the midst thereof He set soul, which He stretched throughout the whole of it; therewith He enveloped also the exterior of its body; and as a circle revolving in a circle He established one sole and solitary Heaven, able of itself because of its excellence to company with itself and needing none other beside, sufficing unto itself an acquaintance and friend. And because of all this He generated it to be a blessed God..” (34-b.)
This spherical form, Timaeus explains, expresses not only the goodness and perfection of a universe patterned from reason and intelligence, but it also expresses the motions of the visible objects in the heavens as well. These visible objects, whose individual motions trace circular arcs onto the celestial sphere, form the “moving image of eternity” we call time. Timaeus proceeds to recount, in detail, the diverse motions of these celestial objects, the totality of which are visible expressions of that which is eternal and universal.
But Plato emphasized that these characteristic spherical motions, while a means to express the characteristics of an idea, cannot, by themselves, be taken as knowledge of the idea. But, being patterned after the eternal, their study can aid us in grasping what can only be apprehended by reason and thought:
“Thus, said I. These sparks that paint the sky, since they are decorations on a visible surface, we must regard, to be sure, as the fairest and most exact of material things, but we must recognize that they fall far short of the truth, of the movements, namely of real speed and real slowness in true number and in all true figures both in relation to one another and as vehicles of the things they carry and contain. These can be apprehended only by reason and thought, but not by sight, or do you think otherwise?
By no means, he said.
Then, said I, we must use the blazonry of the heavens as patterns to aid in the study of those realities, just as one would do who chanced upon diagrams drawn with special care and elaboration by Daedalus or some other craftsman or painter. For anyone acquainted with geometry who saw such designs would admit the beauty of the workmanship, but, would think it absurd to examine them seriously in the expectation of finding in them the absolute truth with regard to equals or doubles or any other ratio.” (Rep. 529e-530b)
The Boundaries of the Sphere
Because these visible expressions could also mislead reason, Plato cautioned against the methods of the Sophists and Eleatics, (forerunners of today’s mathematical formalists and information theorists), whose practice, like their modern counterparts, was to induce insanity in their victims by restricting their attention to the visible form of mathematical objects that have been disconnected from the universal principles from which they arose, and, from the ideas whose shadows they were intended to represent. As he warned in the {Republic}:
“This at least, said I, will not be disputed by those who have even a slight acquaintance with geometry (earth-measure), that this science is in direct contradiction with the language employed in it by its adepts.
How so? he said.
Their language is most ludicrous, though they cannot help it, for they speak as if they were doing something and as if all their words were directed toward action. For all their talk is of squaring and applying the adding and the like, whereas in fact the real object of the entire study is pure knowledge.
This is absolutely true, he said.
And must we not agree on a further point?
What?
That it is the knowledge of that which always is, and not of a something which at some time comes into being and passes away.
That is readily admitted, he said, for geometry is the knowledge of the eternally existent.” (Rep. 527a.)
The Sophists insisted that geometry could state nothing truthful concerning “knowledge about that which always is” because geometrical objects, being objects of sense, lie in the domain of that which is always changing. Consequently for the sophist, geometrical objects, like all other objects of sense, could be connected to each other by a set of formal rules, described and manipulated, but such actions were {by definition} divorced from the eternal physical principles governing the universe itself. By limiting scientific inquiry to such objects of sense perception, as Aristotle also maintained, the Sophists could awe their audiences with dazzling demonstrations, such as the simultaneous existence and non-existence of the one and the many, while convincing them that knowledge of universal principles was, in the end, beyond their grasp.
By contrast, the Pythagorean-Platonic scientists admitted no objects into geometry that did not arise in connection with an effort to grasp an unseen, eternal, universal principle. Such objects, such as the Pythagorean concept of the sphere, were brought into existence by an action of a mind intending to gain greater mastery over the principles that govern the universe itself. Consequently for these Socratics, all such geometrical objects are representations of ideas that are apprehensible only by reason and thought. “Thought-objects” so generated contain within them, the essential characteristics of the universal principles they are intended to grasp. Being thus connected to universal principles, paradoxes generated by the investigation of such objects, point to the existence of unknown principles, that, once discovered, lead to the generation of new ideas, that demand new types of geometrical expression.
In the science of Classical Greece, this is exemplified by the uniqueness of the five regular solids. Nothing in the smooth, everywhere same, form of a sphere gives any indication of the existence of a bounding principle that determines that there be five, and only five, unique solids that equally divide that everywhere constant surface. But, the fact that only five such solids can be constructed, reveals the existence, and reflects the characteristics, of that bounding principle. Thus, even though the sphere is the shape “that comprises all shapes”, the five regular solids indicate the existence of a still higher principle from which the sphere’s power is derived. This higher power, though outside the visible boundary of the sphere, is, nevertheless, expressed on the sphere’s surface, by the uniqueness of the five regular solids.
That that higher principle can be found only by surpassing the boundaries of the sphere, was already evident to the Pythagoreans, as indicated by Archytas’s construction for the doubling of the cube by the intersection of a torus, cylinder and cone. This stands in contrast to the doubling of the square, whose generating principle can be expressed by circular action existing within the same manifold (plane) in which the square itself is generated. On the other hand, the cube, which is formed in the sphere, cannot be doubled by means of spherical action. As Archytas demonstrated, a more complex unfolding of the sphere is required. Thus, the characteristic of the cube, as well as the other four regular solids, indicated to the Pythagoreans and Plato, the existence of a still higher principle that bounds the apparently self-bounded spherical form.
Because of paradoxes like these, Plato insisted that the study of these solids should be emphasized, in addition to the Pythagorean quadrivium of arithmetic, geometry, astronomy and music, in the education of political leaders, so that those leaders could develop the cognitive powers to recognize universal principles and act only on the basis of truth, not on the basis of arbitrary opinion.
For opposing reasons, Aristotle introduced the arbitrary fiction that the form of the universe is an unbounded, empty, linearly extended void, as codified in the Elements of Euclid. Under this scheme, spherical action is not the reflection of the universal principles from which it is generated. It is but only one, of infinitely many undifferentiated possible types of action. For Euclid, the sphere’s existence, like the rest of the objects of Euclidean geometry, rests only on the authority of an {a priori} set of definitions, axioms and postulates. For Euclid, and those indoctrinated by sophism, empiricism, etc. this false, fantasy world of linear action becomes the only true one from which all physical processes deviate.
Ironically, the Pythagorean-Platonic method expressed as self-bounded spherical action reflects the unlimited potential for the discovery of new physical principles, because the existence of these new principles is indicated through the emergence of paradoxes, such as the uniqueness of the five regular solids. On the other hand, the Aristotelean-Euclidean fantasy of an apparently unbounded, linearly extended void, that, {by definition}, permits no physical principles within its midst, acts as a barrier to the introduction of new ideas, restricting human knowledge to a definite and finite domain: a barrier that held back human progress for nearly 1500 years, from the murder of Archimedes in 231 B.C. until the dawn of the European Renaissance in the 14th century.
In sum: the self-bounded is unlimited potential; the unbounded is forever constrained.
Surpassing the Boundaries of the Self-Bounded Sphere
The Aristotelean barrier was cracked when Nicholas of Cusa re-introduced the Pythagorean-Platonic concept of spherics, in the new, more advanced form of his method of “On Learned Ignorance”. Like his forerunners, Cusa understood that mathematical objects, generated as metaphors, were a means for expressing new discoveries:
“Therefore, in mathematicals the wise wisely sought illustrations of things that were to be searched out by the intellect. And none of the ancients who are esteemed as great approached difficult matters by any other likeness than mathematics….
“Proceeding on this pathway of the ancients, I concur with them and say that since the pathway for approaching divine matters is opened to us only through metaphors, we can make quite suitable use of mathematical signs because of their incorruptible certainty.”
Cusa’s approach was emphatically anti-Aristotelean. Instead of the unlimited, linearly extended infinite void, in which geometrical objects rattled around, devoid of intention, Cusa saw the apparent infinite merely as the domain of yet to be discovered universal principles, that bounded the finite and determined the characteristic of action within it. The characteristics of that set of principles can be discovered by ascending upward from their finite manifestation towards the higher expression:
“…when we set out to investigate the Maximum metaphorically, we must leap beyond simple likeness. For since all mathematicals are finite and otherwise could not even be imagined; if we want to use finite things as a way for ascending to the unqualifiedly Maximum, we must first consider finite mathematical figures together with their characteristics and relations. Next, we must apply these relations in a transformed way, to corresponding infinite mathematical figures. Thirdly, we must thereafter in a still more highly transformed way, apply the relations of these infinite figures to the simple Infinite, which is altogether independent even of all figure. At this point our ignorance will be taught incomprehensibly how we are to think more correctly and truly about the Most High as we grope by means of a symbolism.”
Cusa’s approach redefined the self-bounding characteristic of the Pythagorean sphere. For Cusa, the visible sphere, though apparently self-bounded, was actually bounded by a higher domain of universal principles that lay outside the sphere itself. Because the domain of these principles exists outside the domain of finite physical objects, it appears, from the finite perspective of the objects, to be infinitely far away.
Thus, the characteristics of the visible sphere, most importantly for Cusa, the incommensurability between the spherically curved and the linearly straight, reflected the higher principle from which the curved and the straight were both generated. Thus, for Cusa, in opposition to Aristotle, the curved was not a deviation from straightness. Rather, the incommensurability between them, reflected one single principle, in unfolded form. Cusa expressed this relationship by the ironical juxtaposition of the idea of a finite sphere and line with an hypothesized infinite one:
“I maintain, therefore, that {if} there were an infinite line, it would be a straight line, a triangle, a circle and a sphere. And likewise {if} there were an infinite sphere, it would be a circle, a triangle, and a line.” (emphasis added).
From this standpoint, Cusa redefined the physical expression of Pythagorean spherics. There are no perfectly circular or spherical motions in the created world, Cusa correctly insisted. Nor is there perfect equality in harmonics, statics, or other physical phenomena. There is no absolute center to the universe, nor is there a single set of poles. However, this imprecise nature of the physical world does not indicate its deviation from the false-perfection of the {a priori} linearly-extended fantasy world of Aristotle’s Euclidean-type geometry. Rather, this imprecision indicated the characteristics of the true physical-geometry of the universe, which cannot be described by simple abstract geometrical shapes, but must be discovered by physical investigations:
“Thereupon you will see through the intellect, to which only learned ignorance is of help that the world and its motion and shape cannot be apprehended. For the world will appear as a wheel in a wheel and a sphere in a sphere having its center and circumference nowhere, as was stated.”
But, the fact that the physical universe cannot be described by simple, static shapes, does not make it unknowable. It is through this very imprecision, as projected into the visible domain, (as for example, onto the Pythagorean sphere) that the true higher ordering principle can be discovered, as knowledge of the Creator’s intention:
“Who would not admire this Artisan, who with regard to the spheres, the stars, and the regions of the stars used such skill that there is though without complete precision both a harmony of all things and a diversity of all things? This Artisan considered in advance the sizes, the placing, and the motion of the stars in the one world; and He ordained the distances of the stars in such a way that unless each region were as it is, it could neither exist nor exist in such a place and with such an order nor could the universe exist….”
“But all things reply to him, who in learned ignorance asks them what they are, or in what manner they exist, or for what purpose they exist…”
On this basis, Kepler, who called Nicholas of Cusa “divine”, broke the centuries-old barrier that had been established by Aristotelean dogma, and established a new, modern physics not tied to any {a priori} considerations, but only to physical ones. As Kepler noted in the opening of his {New Astronomy}, it may be the first presumption of reason that action in the physical universe is circular, but physical experiment determined this to be untrue. Consequently, all {a priori} geometrical descriptions of the motions of the planets, such as those adopted by Ptolemy, Copernicus, and Brahe must be abandoned in favor of a physical-geometry based only on physical causes. For Kepler, the paradoxes among the tracings of the motions of the planetary orbits onto the celestial sphere provided the clues that led him to discover the principles that were determining them. Thus, Kepler investigated not the objects of the sky, nor simply their motions as projected onto the celestial sphere. Rather, he investigated the relationships between these projected motions, from which he apprehended the characteristics of the unseen principles from which those motions were determined.
It is from this standpoint that Kepler was able to elaborate the harmonics of the non-uniform, essentially elliptical motion of the planetary orbits, giving an entirely new meaning to the physical significance of the ancient Pythagorean discoveries concerning the boundaries of spherical action, such as the five regular solids, conic sections, and musical harmonics. The question posed by Kepler to all future generations, was to develop a new type of mathematics that could express these higher principles. Standing on Leibniz’s shoulders, this is what Gauss and Riemann developed as the complex domain.
The Physical “Shape” of the Universe
As Riemann emphasized in his 1854 habilitation lecture, his philosophical fragments, and his lectures on Abelian and hypergeometric functions, and as Gauss had spoken earlier, the common, intuitive notions concerning geometrical objects presupposes a set of assumptions concerning the fundamental nature of the “space” in which those objects arise. Like Cusa, Kepler, and Leibniz before them, both Gauss and Riemann insisted it was the action of physical principles that determined the characteristics of what is called “space”, not a set of arbitrary {a priori} assumptions. While these physical principles are unseen, the effect of their action is measurable.
To express the connection between these measurable effects and the unseen principles themselves, Gauss and Riemann developed a new form of spherics, by extending Leibniz’s infinitesimal calculus into the complex domain.
For Gauss this meant rejecting all arbitrary notions of the sphere as a three-dimensional object bouncing around in an empty, linearly-extended void. Instead, Gauss considered the sphere to be what Riemann would later call, a doubly-extended manifold. In this way, Gauss eliminated from the sphere (and all other doubly-extended manifolds), all arbitrary ideas of linear extension. Linear distance between any set of points on the surface is determined solely as a function of angular displacement. The relationship between angular displacement and linear extension reflected the effect of an invariant characteristic of the surface. That characteristic Gauss called “curvature”.
By “curvature” Gauss did not mean “not-straight”. Gauss’s idea of “curvature” is an expression of the characteristic principles that determine action on that surface. But, since the characteristic curvature is not visible, it must be discovered by its effect on all action on that surface.
For example, the elliptical arc of a planetary orbit is determined by the harmonic characteristics of the principle of universal gravitation. To the planet, such an arc is a “straight-line”. To our senses the planet’s orbit is a variable arc of a great circle on a sphere. But to our minds, as Kepler showed, we can discover that those arcs are merely the projection onto a sphere of an action that is occurring in a different surface a surface we cannot see. However we can imagine this other surface, not as a visible image, but as that set of physical principles which has the power to produce the physical effects whose visible images are projected onto the celestial sphere. Furthermore, since we are moving in that surface ourselves, we must apprehend its characteristic curvature, from within it, by measuring the effect of that curvature in the relatively infinitesimally small–a method that Leibniz called “analysis situs”.
Gauss’s idea of a surface, therefore, is not a simple visible shape but a manifold of physical principles. To better determine the characteristics of these manifolds, Gauss developed the means to map these manifolds onto a sphere. Under these mappings the characteristic curvature of the unseen surface is expressed as anomalies within the domain of spherical functions. Working backwards, we can then “unfold” these projections, to determine the characteristics of the manifold from which they are projected. (See Riemann for Anti-Dummies Parts 44-46.)
The Riemann Sphere
Armed with Gauss’s work, Riemann generalized the method. As indicated in his fragment on “n-dimensional” manifolds, Riemann considered the geometrical ideas of line, surface and solid as only special intuitive examples of a singly, doubly and triply extended manifold, whose modes of determination are physical principles, not linear extensions. However, Riemann emphasized as did Gauss, Leibniz, Kepler, Cusa, and Plato before him, that the construction of the appropriate metaphorical representation was essential to achieve a greater understanding of these principles, and to communicate these discoveries to others, so as to bring them under the willful control of mankind.
Riemann developed these ideas in his lectures on Abelian and hypergeometric functions, whose deeper implications were not realized until LaRouche’s more advanced, revolutionary breakthroughs in the science of physical economy.
Riemann’s starting point was Gauss’s original idea that the physical characteristics of doubly-extended manifolds, (i.e. surfaces) could be represented in the complex domain as functions of complex numbers. This is based on Gauss’s idea of representing complex numbers as a function of position on a surface.
This is {not} the idea of representing complex numbers as points on an abstract Cartesian grid as is universally taught in reductionist mathematics education today. We emphasize, as Gauss did, that any function of position must be in reference to some physically determined starting point and a physically determined direction. For example, the determination of position on the celestial sphere, must be in reference to some starting point (the pole), and some direction (the direction of the position of sunrise on the vernal equinox). Once these two parameters (origin and direction) are determined, all other positions on the surface can be expressed with respect to them. This is distinct from the Aristotelean, Euclidean, Cartesian, Kantian idea of an undifferentiated, linearly-extended space. As Gauss pointed out with reference to Kant, it is impossible to determine anything about the nature of space except by reference to physical objects. In other words, Gauss did not begin with a Cartesian-Kantian idea of an empty surface and then assign some arbitrary origin and direction to it. Rather, physics establishes the origin and reference direction, which in turn established the surface.
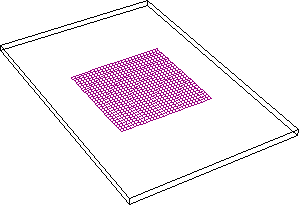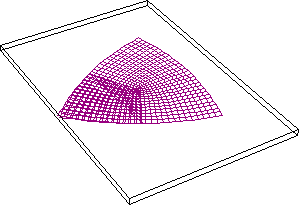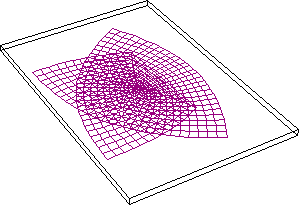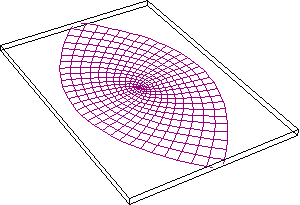
Riemann showed that once such a physically determined doubly-extended surface has been established, the characteristics of action within that surface can be expressed as a complex function. Here again, Riemann adopted Gauss’s approach of the “Copenhagen Prize Essay” on conformal mappings. For example, the stereographic projection of the sphere onto the plane is an expression of the complex exponential. (See Figure 1.)
|
Figure 1 |
Thus, complex functions considered as conformal mappings, express the transformation of one surface, with a certain characteristic of action, into another, with a different characteristic of action.
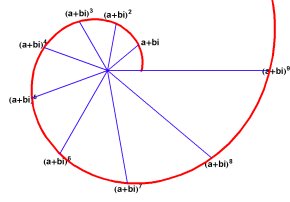
For pedagogical purposes let us investigate this matter in more detail with respect to the ancient Pythagorean problem of doubling the square, as seen from the higher perspective of the complex domain. As Gauss demonstrated in his new proof of the fundamental theorem of algebra, the most general expression of an algebraic power is represented geometrically as a specified change in angle and length. That is, squaring is expressed by doubling the angle and squaring the length with respect to that physically determined origin and direction. Cubing is expressed by tripling the angle and cubing the length, etc. (See Figure 2.)
|
Figure 2 |
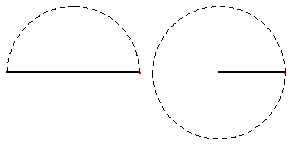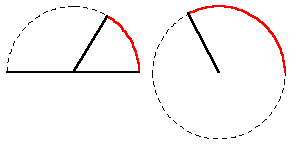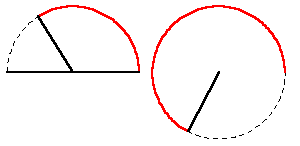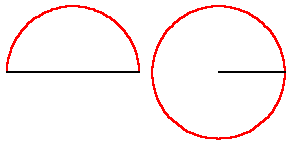
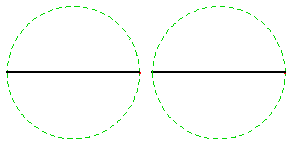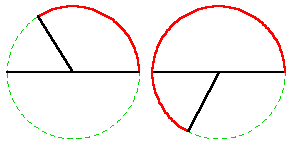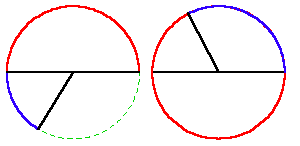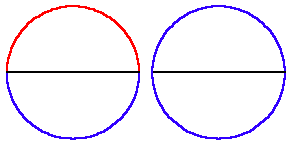
So, for example, in the simplest case of squaring as a complex function, a semi-circular pathway will be mapped onto a full circle. (See Figure 3.)
|
Figure 3 |
Thus, a complete circle will be mapped onto a complete circle twice. (See Figure 4.)
|
Figure 4 |
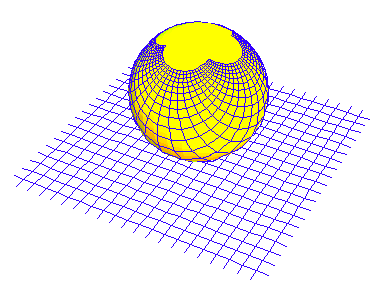
Transforming an entire surface in this way, thus maps half the original surface on top of the other. (See Figure 5.)
|
Figure 5 |
Since it is impossible, in a Cartesian empty space, to distinguish the first mapping from the second, Riemann invented the idea of a surface that has two layers with the second mapping laying on top of the first. Thus, by squaring, every point on the original surface is transformed into two different points, one laying directly over the other, on the “squared” surface. Those points that have only one value (in this example, the origin), Riemann called a “branch point”. (See Figure 6.) These branch points correspond to physical singularities on the surface as the characteristic of action with respect to them is different than the rest of the surface. A surface with no branch points, Riemann called, “simply-connected”; a surface with one branch point he called “doubly-connected”; a surface with two branch points he called “triply-connected”, etc.
|
Figure 6 |
Riemann emphasized that this type of mapping can not occur in a linear, infinitely-extended surface, but only in a bounded one. The reader is encouraged to discover this for yourself. You will discover that it is impossible to think of transforming one doubly-extended manifold (i.e. surface) into another without a boundary. Even if the nature and characteristics of that boundary are not yet determined, its necessary existence is.
This is another indication of why physical action can only be expressed in the complex domain, as there is no physical process that is not bounded. For this reason, Riemann insisted that one could not express complex functions on a Cartesian plane, but only on a bounded surface, as represented by what today is called, “The Riemann Sphere”. (See Figure 7.)
|
Figure 7 |
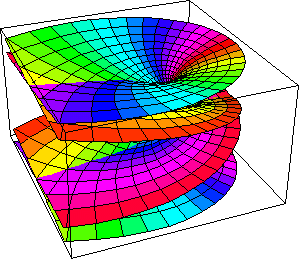
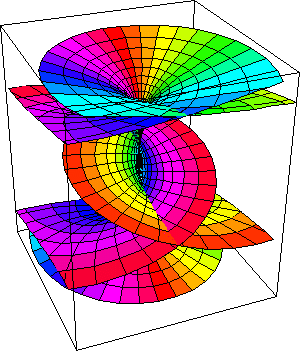
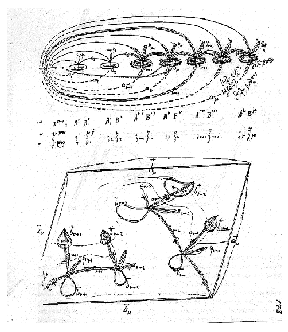
Now, back to Riemann’s surfaces. Riemann confronted the problem that when a mapping produces a multi-sheeted surface, a paradox results, because a continuous curve on one surface becomes two separate curves on two (or more) different layers of the second surface. For this reason he specified the need for a cut, which he called a “branch-cut” that extended from the branch points to the boundary. The various layers of the surface are then connected to one another along these branch cuts, so that all pathways on one of the layers can be continued onto all the other layers continuously. (See Figures 8a, 8b, 8c, 8d, and 8e. These figures include some computer generated representations as well as a hand drawn representation by Riemann himself.)
|
Figure 8a |
Figure 8b |
|
Figure 8c |
Figure 8d |
|
Figure 8e |
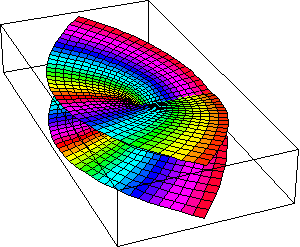
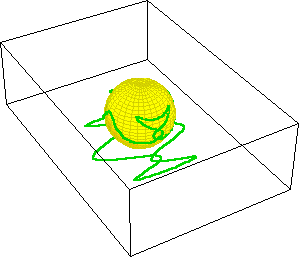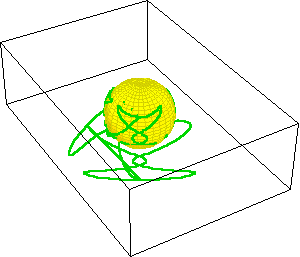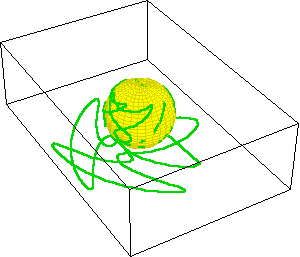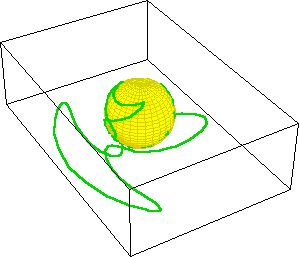
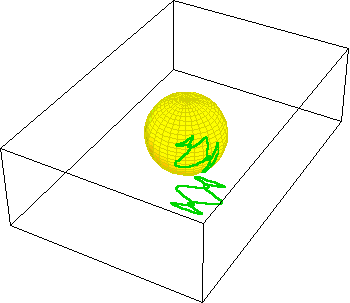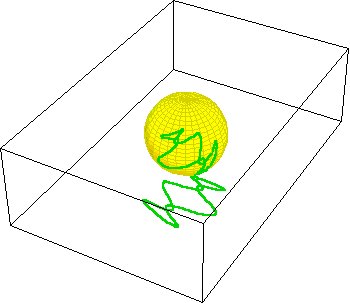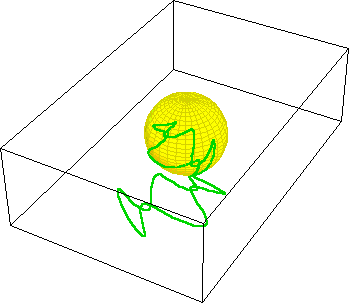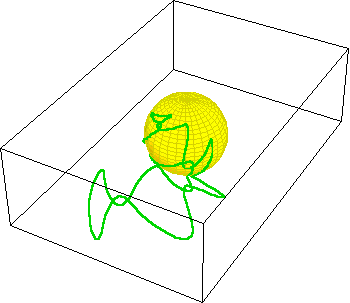
On the Riemann sphere, the entire function can be represented because unlike the Cartesian plane which has no boundary, the Riemann sphere is bounded. The accompanying animation, (See Figure 9.) illustrates the squaring function projected onto Riemann’s sphere. As the boundary on the plane extends outward from the origin, its projection approaches the “north pole” of the sphere. In this example, the squaring function forms a two-sheeted surface on the sphere, whose branch cut runs from one pole to the other.
|
Figure 9 |
These animations illustrate the action of the singularity on the Riemann sphere. Here two closed pathways, one encircling the branch point at the origin (10a.) and the other not, (10b.) are illustrated.
|
Figure 10a |
Figure 10b |
Under squaring, the pathway encircling the branch point at the origin folds over itself and is mapped onto two sheets. The pathway that does not contain the branch point remains entirely on one layer. (See Figure 10c.)
|
Figure 10c |
However, something is revealed on the Riemann sphere that would otherwise remain hidden. The sphere reveals the existence of another branch-point at the north pole, which in the Cartesian plane can only be considered “the infinite”. This can be seen by performing the same squaring action, but under the inversion that turns the function “inside out”. What was the origin is now the “infinite” and vice versa. (See Figure 11.) This has the same effect on closed pathways. Inversion turns the pathways inside out, which now encircle the branch point at the “infinite”, or the north pole on the sphere. (See Figure 12.) Just as the branch point at the origin acted as a singularity, so now does the other branch point, that had been hidden in the “infinite” in the Cartesian plane, but on the Riemann sphere it is plainly brought into view.
|
Figure 11 |
Figure 12 |
Beyond the Sphere
On this basis, Riemann was able to demonstrate, using Leibniz’s principle of “analysis situs”, that all the essential characteristics of a complex function, are determined by the relationship of the boundary to the branching points, or the other singularities.
This discovery was crucial to Riemann’s treatment of elliptical and Abelian functions. As we discussed in previous installments (See Riemann for Anti-Dummies Parts 49, 52 and 54) these functions, that initially arose from the investigations of Kepler’s elliptical planetary orbits, express a succession of higher transcendental powers. Riemann demonstrated, using a method similar to the one used by Gauss in his proof of the fundamental theorem of algebra, that those complex functions associated with these higher transcendentals generate surfaces with two sheets, but with more than the two branch points expressed by the algebraic, circular, hyperbolic or exponential functions. (See Figure 13.) As Riemann showed, each successively higher power, generates a new set of branch points.
|
Figure 13 |
For example, as illustrated in the previous installments, Gauss showed that the elliptical transcendentals were distinguished from the circular, hyperbolic, and elliptical, by their double periodicity. (See Figure 14.)
|
Figure 14 |
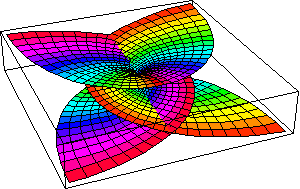
Riemann showed that this characteristic, by necessity, produces four branch points, which require two branch cuts. (See Figure 15.)
|
Figure 15 |
A surface with two branch cuts must be doubly connected, as for example a torus (See Figure 16.) Thus, each new species of transcendental function is characterized by a change in the characteristic topology of the surface, from an “n” connected manifold to an “n+1” connected manifold.
|
Figure 16 |
This is the type of transformation associated with the discovery and application of a new physical principle.
Now looking back from the standpoint of this new type of Riemannian spherics, we can recognize that the Pythagorean spherics, is only the simplest type of a succession of self-bounded surfaces of increasingly higher “connectivity”. The provocative question now posed is: What bounds this succession of self-boundedness?
This same question was posed by Gauss in a different way concerning the determination of what is the true geometry. In a letter to Olbers on April 28, 1817, Gauss asserted, like Cusa, that the true geometry could never be seen directly but must be discovered:
“Perhaps in another life we will come to another insight into the essence of space, which is now unreachable for us. Until then, one must not put geometry with arithmetic, purely a priori, but closer to in rank with mechanics…”